Problem 2
ABCD is a quadrilateral and P is the centre of its incircle. Then, prove that:
ar(PAB) + ar(PCD) = ar(PBC) + ar(PDA)
Here’s a simulation that demonstrates what needs to be proven.
You can drag A, B, and C and observe the two sums of the areas.
Solution
I won’t provide the full solution here, but only give you some tools and hints that’ll help you solve the problem yourself.
So, tangents. You should be knowing two things about them.
First, tangent drawn to a circle at a point is perpendicular to the radius (joining that point to the center).
That is, in the figure below, AB ⊥ CD.

Second, two tangents drawn from an external point to a circle are equal in length.
That is, in the figure below, AB = AC.

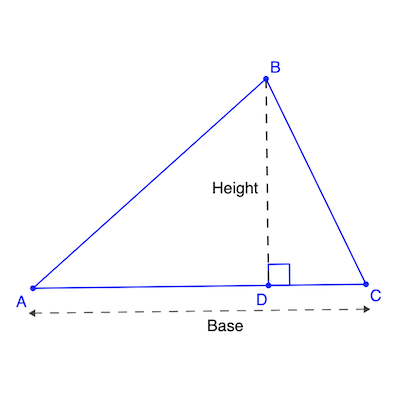
One more thing. You need to know how to find the area of a triangle. Here’s one of the formulas that might help:
Area = 1/2 x Base x Height
That is, in the figure below, the area of the triangle ABC equals 1/2 x AC x BD.
Well, that’s all that you need to know here. I suggest you proceed on your own from this point. Good luck!
Were you able to solve it using the above hints? Or, did you solve using any other method? Or, do you need some more help? You can reach out at the Facebook page.
Problem Source: GoGeometry
Previous Problem | Next Problem | Geometry Problems | Problems Home