Time for some examples involving the point-slope form of the equation of the straight line.
Example 1 Find the equation to the line
(i) whose slope is 3 and which passes through the point (1, 4).
(ii) makes and angle of 135° with the X-axis and passes through the point (2, -3).
Solution In both parts, we’ll directly use the point slope form of the equation, which is
y – y1 = m(x – x1)
(i) We’ve been given the point as well as the slope. By plugging in the values, we get the required equation as:
y – 4 = 3(x – 1)
or
3x – y + 1 = 0
This is what the line looks like.

(ii) In this case, the slope isn’t given. But the angle made with X-axis is given instead. This will help us find the slope:
m = tan135° = -1
Now, let’s use the point slope form again:
(y – (-3)) = -1(x – 2)
On simplifying, we’ll get:
x + y + 1 = 0
Here’s how the line looks.

Example 2 Find the equation of the straight line which bisects the line joining (3, 4) and (5, 2), and makes an angle 60° with the X axis.
Solution Here, the slope equals tan60° or √3.
A little extra effort is required in finding out the point through which the line passes. The point will be the mid-point of (3, 4) and (5, 2), which is:
((3 + 5)/2, (4 + 2)/2) or (4, 3)
And, the required equation is
y – 3 = √3(x – 4)
or
√3x – y – 4√3 + 3 = 0
Here’s how the line looks.
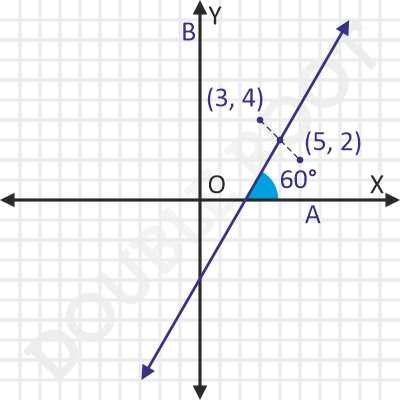
That’s it for these examples. The next lesson will cover another useful form of the straight line’s equation, known as the two-point form.