This lesson will talk about number of common tangents to two given circles. This will depend upon the relative position of the two circles – something which I talked about in the previous lesson. Let’s revisit all the cases.
Lying Outside Each Other
In this case, there will be four common tangents. Have a look.
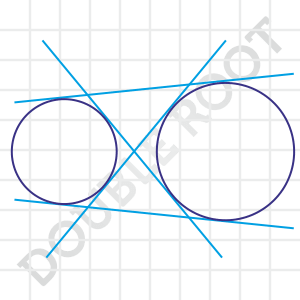
The tangents intersecting between the circles are known as transverse common tangents, and the other two are referred to as the direct common tangents.
Touching Each Other Externally
In this case, there will be three common tangents, as shown below.
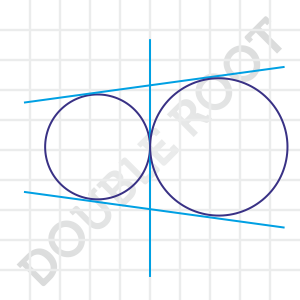
The tangent in between can be thought of as the transverse tangents coinciding together.
Intersecting Each Other at Two Points
In this case, there will be two common tangents.

Touching Each Other Internally
In this case, there will be only one common tangent, as shown in the figure.

Think of is as the two tangents in the previous case coinciding into one, when one of the circles is pushed towards the other.
One Lying Inside Another
In this case, there will be no common tangent, as any line touching the inner circle will always intersect the outer circle at two points.

Here’s a simulation that shows the common tangents to two circles.
You can drag the four blue points, and observe the number of common tangents to the two circles. Does this align with what we discussed above?
Lesson Summary
I’ve summarised the lesson in the following table:
Position |
Number of Common Tangents |
| Lying outside each other | 4 |
| Touching externally | 3 |
| Intersecting at two points | 2 |
| Touching internally | 1 |
| One lying inside other | 0 |
In the next lesson, I’ll talk about the equations of these common tangents.