Summary
This math recipe will help you find the slope of a line in the XY Plane, whose equation is known.
Skill Level
Easy
Time
Approx. 15 sec
Ingredients
Equation of the line: \(ax + by + c = 0\)
Method
To determine the slope (\(m\)) of the line, we’ll use the following formula
\(m = –\frac{b}{a}\)
Examples
Example 1 Find the slope of the line \(3y = 4x + 12\).
Solution First, we’ll rearrange the terms to make the equation of the form \(ax + by + c = 0\). We’ll get
\(–4x + 3y – 12 = 0\)
Now, we’ll use the formula for the slope:
\(m = –\frac{–4}{3} = \frac{4}{3}\)
Therefore, the slope of the line equals \(\frac{4}{3}\). The following figure shows the line on the \(XY\) plane.

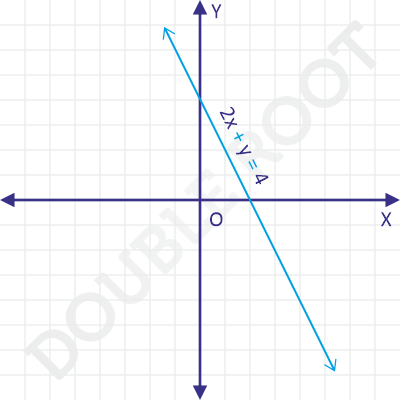
Example 2 Find the slope of the line \(2x + y = 4\).
Solution We’ll first rearrange the terms of the equation to get:
\(2x + y – 4 = 0\)
Now, let’s use the formula for the slope:
\(m = –\frac{2}{1} = –2\)
Therefore, the slope of the line equals \(–2\). The following figure shows the line on the \(XY\) plane.
Example 3 Find the slope the line \(3y – 6 = 0\).
Solution The equation can be rewritten as:
\(0x + 3y – 6 = 0\)
Now, let’s use the formula for the slope:
\(m = –\frac{0}{3} = 0\)
Therefore, the slope of the line equals \(0\). The following figure shows the line on the XY\) plane.

Example 4 Find the slope of the line \(2x = 8\).
Solution Let’s rearrange the equation first. We’ll get:
\(2x – 8 = 0\) or \(2x + 0y – 8 = 0\)
Now, let’s use the formula given above:
\(m = –\frac{2}{0}\), which is undefined.
Therefore, the slope of the line is undefined. The following figure shows the line on the \(XY\) plane.

That’s it for this recipe. Hope you found it helpful.
For more recipes, please visit www.doubleroot.in/recipes.
You can follow me on Instagram, Twitter, or Facebook to get all updates.