Distance Between Parallel Lines

Summary

This math recipe will help you find the distance between two parallel lines the XY plane.

Skill Level

Easy

Time

Approx. 1 min

Ingredients

Equations of the parallel lines: ax + by + c₁ = 0 and ax + by + c₂ = 0

If the lines are not in the above form, we’ll first need to transform them by bringing all terms to the same side and/or multiplying either of them with a constant.

Method

To find the distance d between the parallel lines, we’ll use the following formula:

d = |c₂ – c₁| / √(a² + b²)

Examples

Example 1 Find the distance between the lines 4x + 3y – 5 = 0 and 4x + 3y = 10.

Solution To apply the formula, yhe second equation needs to be rewritten as:

4x + 3y – 10 = 0

To find the distance, we’ll apply the above formula. The required distance equals:

|(-5) – (-10)| / √(4²+3²)

= |5| / 5

= 1

Here’s a figure to illustrate.

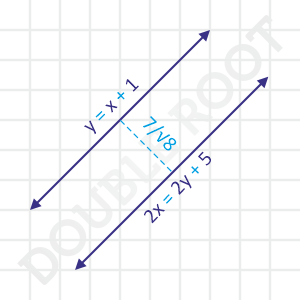
Example 2 Find the distance between the lines y = x + 1 and 2x = 2y + 5.

Solution To apply the formula, we’ll need to tranform the two equations as:

x – y + 1 = 0

2x – 2y – 5 = 0

Next, we should tranform either equation so that the corresponding coefficients of x and y in both equations are the same. To do that, we’ll multiply the first equation by 2, to get:

2x – 2y + 2 = 0

Now, we can find the distance between the two lines, which equals:

|2 – (–5)| / √(2²+(-2)²)

= 7/√8

That’s it for this recipe. Hope you found it helpful.

For more recipes, please visit www.doubleroot.in/recipes.

You can follow me on Instagram, Twitter, or Facebook to get all updates.