Summary
This math recipe will help you find the area of a triangle, coordinates of whose vertices are known.

Skill Level
Easy
Time
Approx. 2 min
Ingredients
Coordinates of the three vertices: \(A(x_1, y_1)\), \(B(x_2, y_2)\), and \(C(x_3, y_3)\)
Method
To find the area of \(\Delta ABC\), we’ll simply plug their coordinates into the formula below:
Area \( = \frac{1}{2}|x_1(y_2 – y_3) + x_2(y_3 – y_1) + x_3(y_1 – y_2)|\)
Examples
Example 1 Find the area of the triangle, whose vertices are \(P(4, 6)\), \(Q(-2,2)\), and \(R(1, 1)\).
Solution The figure shows \(\Delta PQR\) on the XY plane.

To find the area, we’ll use the above formula directly.
Area \(= \frac{1}{2}|4(2 – 1) –2(1 – 6) + 1(6 –2)|\)
\(= \frac{1}{2}|4(1) – 2(–5) + 1(4)|\)
\(= \frac{1}{2}|4 + 10 + 4|\)
\(= \frac{1}{2}|18|\)
\(= 9\ sq. units\)
Example 2 Find the area of the triangle, whose vertices are \(A(-1, 5)\), \(B(7, -3)\), and \(C(0, -2)\).
Solution The figure shows \(\Delta ABC\) on the XY plane.
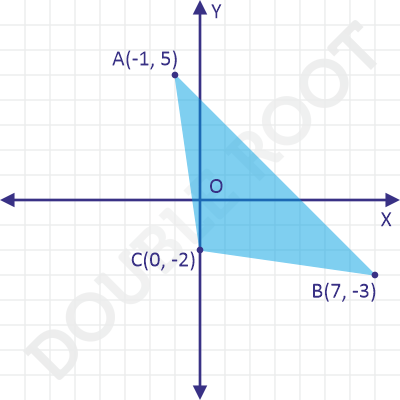
To find the area, we’ll again use the above formula.
Area \(= \frac{1}{2}|–1(–3 – (–2)) + 7(–2 – 5) + 0(5 – (–3))|\)
\(= \frac{1}{2}|(– 1)( –1) + 7(–7) + 0(8)|\)
\(= \frac{1}{2}|1 – 49 + 0|\)
\(= \frac{1}{2}|– 48|\)
\(= 24\ sq. units\)
That’s it for this recipe. Hope you found it helpful.
For more recipes, please visit www.doubleroot.in/recipes.
You can follow me on Instagram, Twitter, or Facebook to get all updates.