Angle Between Two Lines

This math recipe will help you find the angle between two lines, whose slopes are known.

Easy

Approx. 1 min

Slopes of the two lines: m₁ and m₂

To determine the angle (θ) between the lines, we’ll use the following formula

tanθ = |(m₁ – m₂)/(1 + m₁m₂)|

Example 1 Find the angle between the lines, whose slopes are 1/2 and -1/3.

Solution To find the angle, we’ll use the above formula

tanθ = |{1/2 – (-1/3)} / {1 + (1/2)(-1/3)}|

= |(5/6) / (5/6)|

= 1

⇒ θ = π/4

The figure shows the two lines.

Example 2 Find the angle between the lines, whose equations are 2x + y = 6 and 4x + 2y = 4.

Solution First, we’ll find the slopes of these lines (using this recipe).

For the line 2x + y = 6, the slope m₁ equals -3/1 or -2.

For the line 4x + 2y = 4, the slope m₂ equals -4/2 or -2.

Using the formula above, the angle between these two lines is given by

tanθ = |{-2 – (-2)} / {1 + (-2)(-2)}|

= |0/5|

= 0

⇒ θ = 0 (implying that the lines are parallel)

The figure shows the two lines.

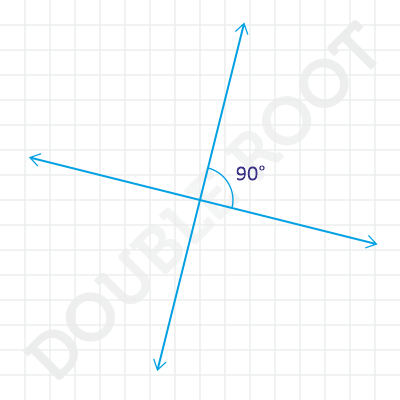
Example 3 Find the angle between the lines, whose slopes are 4 and -1/4.

Solution Using the formula above, the angle between these two lines is given by

tanθ = {(4 – (-1/4)} / {1 + 4 x (-1/4)}|

= |(17/4)/0|, which is undefined.

⇒ θ = π/2 (implying that the lines are perpendicular)

The figure shows the two lines.

That’s it for this recipe. Hope you found it helpful.

For more recipes, please visit www.doubleroot.in/recipes.

You can follow me on Instagram, Twitter, or Facebook to get all updates.