Problem
Let S be the set of all twice differentiable functions f from R to R such that d²f/dx² > 0 for all x ∈ (-1, 1). For f ∈ S, let Xf be the number of points x ∈ (-1, 1) for which f(x) = x. Then which of the following statements is (are) true?
A. There exists a function f ∈ S such that Xf = 0
B. For every function f ∈ S, we have Xf ≤ 2
C. There exists a function f ∈ S such that Xf = 2
D. There does NOT exist any function f in S such that Xf = 1
Solution
The best way to approach this is using an example. I’ll take f(x) = eˣ + a.
The two vertical lines are x = -1 and x = 1, and the diagonal line represents y = x. What we’re looking for is the number of points of intersection of y = f(x) (the blue curve) and y = x.
Try dragging the slider to change the values of a. What do you notice?
When a is greater than -1, the graph of f(x) doesn’t intersect the line y = x. That means Xf = 0 for such values of a, making option A true.
When a equals -1, the graph of f(x) touches the line y = x (this can be easily proven as well). That means Xf = 1 for a = -1, making option D false.
Finally, when a < -1, the two graphs intersect at two points. At a = -1.2 particularly, the two intersection points lie in the interval x ∈ (-1, 1). That means Xf = 1 for this value of a, making option C true.
Seems like option B is also true. But taking an example wont be enough, because this needs to be proven for all such functions.
Or, for B to be false, we need to find a function for which Xf = 3, i.e. the graph of the function intersects the line y = x at 3 (or more) points. Is that possible?
For a concave upwards graph, if we join any two points on it, the entire graph lies below this line segment (or the secant). Take a look.
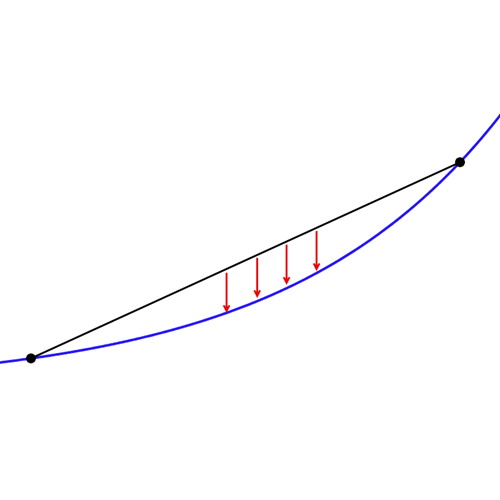
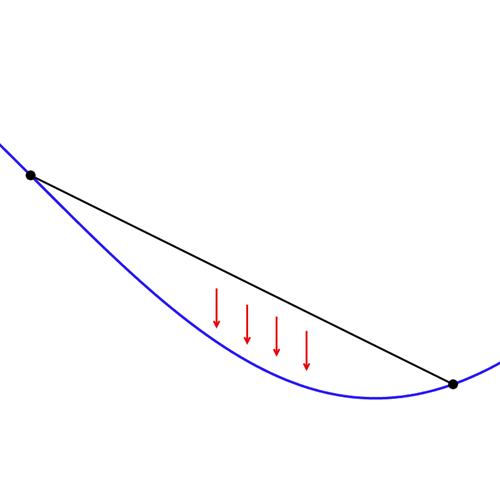
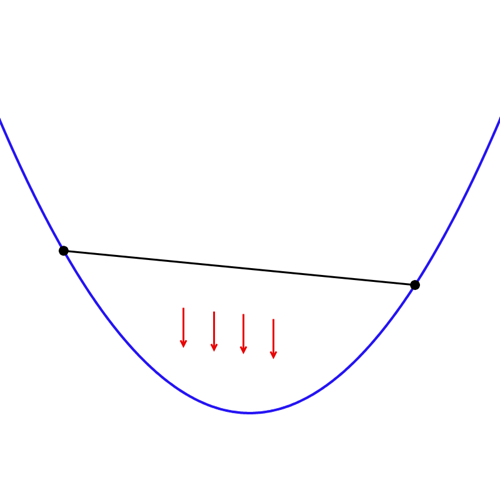
Now, for the function f(x), let’s consider y = x as this secant. Also, let’s assume (a, a) and (b, b) to be the two points of intersection of f(x) and y = x.
Then, for all c ∈ (a, b), f(c) < c (i.e. the graph of y = f(x) lies below the graph of y = x). In other words, f(c) cannot be equal to c for all c ∈ (a, b). Or, there cannot be a third intersection point.
And that makes option B true as well!
We could also assume a point such that f(c) = c, and then prove this to be false by contradiction. Yet another way to prove this is using Rolle’s theorem.
Assume that g(x) = f(x) – x has three distinct roots (i.e. the graph of y = f(x) intersects y = x at three different points). Then, using Rolle’s theorem, g'(x) = f'(x) – 1 must have two distinct roots, and g”(x) = f”(x) must have one root.
But that’s not possible since f”(x) is given to be positive. So, f(x) – x = 0 cannot have three distinct roots. In other words, Xf cannot be 3 or more. Therefore, option B is true.
Comments
A nice, conceptual problem based on calculus. Wasn’t too difficult, but wasn’t too easy either. Drawing a few functions matching the given conditions is a great way to figure out each option. Try taking y = x² + b or any other concave upwards functions as well. Also, what happens if d²f/dx² < 0? Will the same options be valid?