Problem
For any y ∈ R, let cot-1y ∈ (0, π) and tan-1y ∈ (-π/2, π/2). Then, find the sum of all the solutions of the equation tan-1(6y/(9 – y²)) + cot-1((9 – y²)/6y) = 2π/3 for 0 < |y| < 3.
Solution
Let tan-1(y/3) = x. Then, y = 3tanx.
The equation now looks something like this: tan-1(18tanx/(9 – 9tan²x)) + cot-1((9 – 9tan²x)/18tanx) = 2π/3
This simplifies to tan-1(tan2x) + cot-1(cot2x) = 2π/3.
Now, if 0 < y < 3, then 0 < y/3 < 1. And therefore, 0 < x < π/4, or 0 < 2x < π/2.
For this interval, tan-1(tan2x) = 2x and cot-1(cot2x) = 2x.
So, the equation becomes 2x + 2x = 2π/3, which gives x = π/6, and therefore y = √3.
Now, if -3 < y < 0, then -1 < y/3 < 0. And therefore, -π/4 < x < 0, or -π/2 < 2x < 0.
For this interval, tan-1(tan2x) = 2x and cot-1(cot2x) = 2x + π.
So, the equation becomes 2x + 2x + π = 2π/3, which gives x = -π/12, and therefore y = 3√3 – 6.
Finally, the sum of all solutions equals √3 + 3√3 – 6 or 4√3 – 6.
Comments
A fairly simple problem – provided you’re comfortable with handling functions of the form tan-1(tanx), cot-1(cotx) etc. A good way to remember their behavior / values in different intervals is to remember their graphs. For example, here’s the graph of tan-1(tanx).
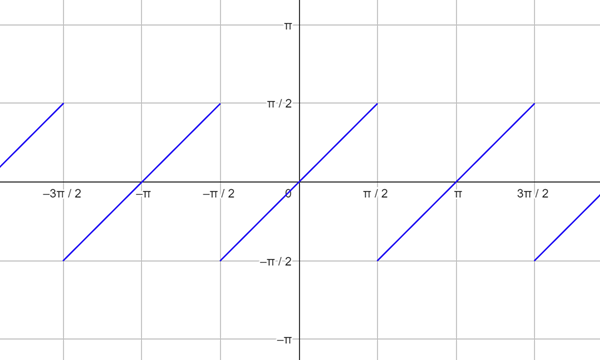
When x ∈ (-π/2, π/2), tan-1(tanx) = x,
When x ∈ (π/2, 3π/2), tan-1(tanx) = x – π.
When x ∈ (-3π/2, -π/2), tan-1(tanx) = x + π, and so on.
Remembering the graph makes it easier to remember the values of such functions in various intervals, and such equations can then be solved without much trouble.