Problem
Consider the 6 × 6 square in the figure. Let A₁, A₂, …, A₄₉ be the points of intersections (dots in the picture) in some order.
We say that Aᵢ and Aⱼ are friends if they are adjacent along a row or along a column. Assume that each point Aᵢ has an equal chance of being chosen.
Let pᵢ be the probability that a randomly chosen point has i many friends, i = 0, 1, 2, 3, 4. Let X be a random variable such that for i = 0, 1, 2, 3, 4, the probability P(X = i) = pᵢ. Then find the value of 7E(X).
Solution
To calculate E(X), we’ll find pᵢ for each value of i and apply the expected value formula, i.e. E(X) = ∑i.pᵢ.
i = 0
If we pick any point, it must have atleast two friends (i.e. a horizontally or vertically adjacent point). In other words, it’s impossible for a point to have 0 friends. So, the probability p₀ must equal 0.
i = 1
As discussed above, if we pick any point, it must have atleast two friends. That is, it’s impossible for a point to have 1 friend. So, the probability p₁ must equal 0 as well.
i = 2
The corner points are the only points to have 2 friends each. Take a look.

So, the probability p₂ equals 4/49 (4 such corner points out of 49 total).
i = 3
The points on the edges (or sides), except the corner points, are the only points to have 3 friends each.

We have 5 such points on each edge, and 4 edges. So 5 x 4 or 20 such points in total. Therefore, the probability p₃ equals 20/49.
i = 4
All remaining points, i.e. apart from the points on the edges or corners, will have 4 friends each. Have a final look.
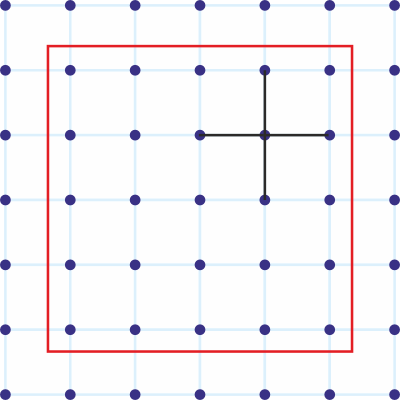
If we discard the edges and corners, we’re left with a 5 x 5 grid of such points. Therefore, the probability p₄ equals 25/49. Time to apply the formula for E(X).
Substituting the values from above, we’ll get E(X) = 2 x 4/49 + 3 x 20/49 + 4 x 25/49 = 168/49.
So, 7E(X) equals 7 x 168/49 or 24.
Comments
The wording of the problem seemed weird somehow. Plus, too many words to communicate a simple idea, especially when the problem itself wasn’t that complicated to solve. Here’s how I would have worded it:
Here’s a grid of points. Two points are said to be neighbors if they are adjacent either horizontally or vertically, as indicated below.
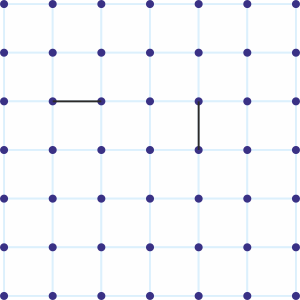
Suppose a point is chosen from the grid at random. Find the expected value of its number of neighbors.
Much more readable! Not sure why it was made so complicated.
That said, the problem itself was easy enough – the counting involved was direct, and so was the application of the expected value formula.