Problem
Let n ≥ 2 be a natural number and f: [0,1] → R be the function defined by
f(x) = \( \begin{cases} n(1-2nx)& \text{ if }\ 0\le x \le \frac{1}{2n} \\ 2n(2nx-1)& \text{ if } \ \frac{1}{2n}\le x \le \frac{3}{4n} \\ 4n(1-nx)& \text{ if }\ \frac{3}{4n} \le x \le \frac{1}{n} \\ \frac{n}{n-1}(nx-1) & \text{ if }\ \frac{1}{n}\le x \le 1 \end{cases} \)
If n is such that the area of the region bounded by the curves x = 0, x = 1, y = 0 and y = f(x) is 4, then find the maximum value of the function f.
Solution
To proceed, we need to find the given area in terms of n, equate it to 4, and find the value of n. Post that we’ll figure out how to find the maximum value of f(x).
To find the area, let’s draw the graph of the function. In each interval, the graph is a line segment, whose end points can be figured out easily. Here’s what the graph looks like.
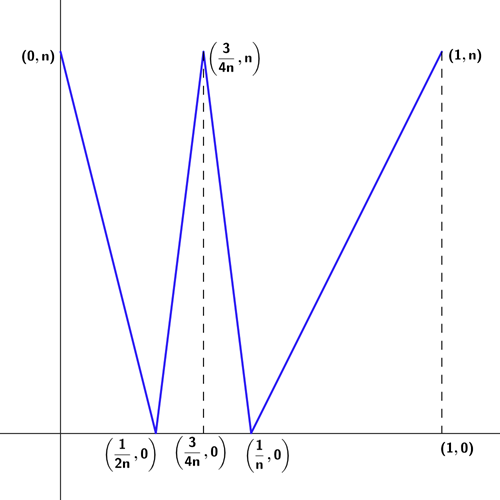
Now, the area bounded by x = 0, x = 1, y = 0 and y = f(x) is nothing but the combined area of the triangles.
Since each of them have the same height, we can add up their bases and multiply the sum by half times the height.
The sum of the bases is 1, and the height is n. So, the combined area equals 1/2 x 1 x n or n/2.
Since this is given to be 4, we’ll get n = 8.
Now, if you go back to the graph again, the maximum value of the function is n.
So, the required answer is n… or 8. And we’re done!
Comments
A simple problem, though the graphing could get a bit tedious. But once you’re done with that, the rest of the problem is a breeze. Some effort was saved in figuring out the bounded area using simple geometry. Integration would have been a waste of time.
\(\)