Problem
Let tan-1x ∈ (-π/2, π/2), for x ∈ R. Then find the number of real solutions of the equation √(1 + cos2x) = √2tan-1(tanx) in the set (-3π/2, -π/2) U (-π/2, π/2) U (π/2, 3π/2).
Solution
An efficient way to count the number of solutions is to graph the functions on both sides. Before that, we’ll simplify things a bit.
1 + cos2x equals 2cos²x. So, the LHS changes to √(2cos²x) or √2|cosx|.
And, the equation simplifies to |cosx| = tan-1(tanx).
Now, the graph of |cosx| is pretty straighforward – we’ll draw the graph of cosx and reflect the part below the x-axis about the x-axis. Here’s what we’ll get.

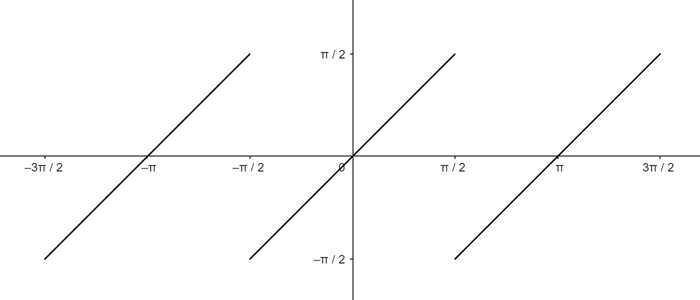
For the graph of tan-1(tanx), we’ll have to define it in different intervals, as follows:
- When x ∈ (-π/2, π/2), tan-1(tanx) = x,
- When x ∈ (π/2, 3π/2), tan-1(tanx) = x – π.
- When x ∈ (-3π/2, -π/2), tan-1(tanx) = x + π, and so on.
Using the above, we’ll get the following graph.
Now, let’s plot both the graphs together to count the solutions.

Three solutions. And, we’re done!
Comments
A simple problem involving two graphs and their intersection points. We could also have solved the problem analytically, but the graphs were pretty straightforward and the intersection points were easy to find.
Also, since we didn’t have to find these solutions, actually solving the equation should to be avoided in such situations. Solving this particular equation wasn’t straightforward anyways, since it involved trigonometric functions on one side and algebraic on the other.