Problem
Let Q be the cube with the set of vertices {(x₁, x₂, x₃) ∈ R³ : x₁, x₂, x₃ ∈ {0, 1}}. Let F be the set of all twelve lines containing the diagonals of the six faces of the cube Q. Let S be the set of all four lines containing the main diagonals of the cube Q; for instance, the line passing through the vertices (0, 0, 0) and (1, 1, 1) is in S. For lines l₁ and l₂, let d(l₁, l₂) denote the shortest distance between them. Then, find the maximum value of d(l₁, l₂), as l₁ varies over F and l₂ varies over S.
Solution
Let’s start by drawing any one ‘main’ diagonal of the cube. That will be enough for us, since each main diagonal can be translated into one another by rotating the cube.
Next, out of the 12 ‘face’ diagonals, there will be 6 that intersect this main diagonal (at the vertices).
Let’s take a look at just one of them first.
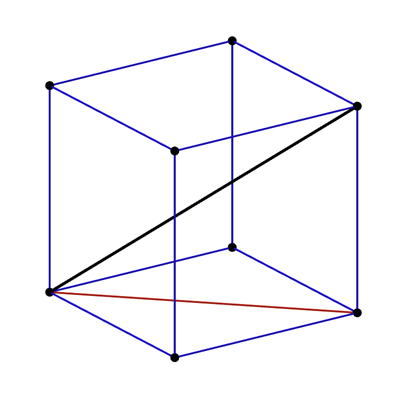
And, here are all the 6 together.
Try rotating the cube and observe the symmetry. Will each main diagonal will have 6 such corresponding face diagonals?
Now, the distance between each of these face diagonals and the main diagonal is 0.
Can the distance get larger than this? What about the remaining 6 face diagonals? Let’s draw one of them.

This time, the two diagonals do not intersect. What about the remaining 5? Let’s see them together!
Again, due to symmetry, the distance between each of the face diagonals and the main diagonal is the same. Try rotating the cube to observe this.
So, this is the so-called maximum distance that we need to find.
The rest of the problem is pretty straight-forward – we just need to apply the shortest distance formula. Let’s label the points.
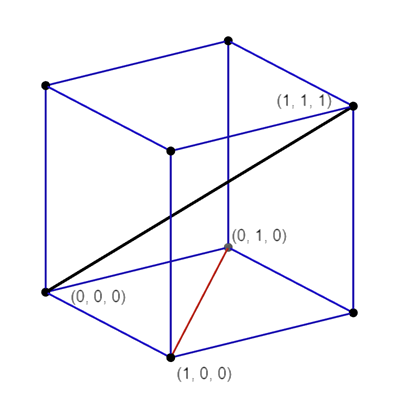
We’ll use the vector form of the equation of each diagonal.
The equation of the main diagonal is r = λ(i + j + k), and of the face diagonal is r = i + μ(i – j).
Now, using the shortest distance formula, we’ll get the required distance as i.[(i + j + k) x (i – j)]/|(i + j + k) x (i – j)|.
This simplifies to i.(i + j – 2k)/|i + j – 2k|, which equals 1/√6.
Comments
The problem was a pain to read – unnecessarily complicated by so much notation. But once you figure out the symmetry, it’s pretty easy to solve – a direct application of the shortest distance formula. Also, there was no ‘maximization’ involved, since the distance between l₁ and l₂ from the respective sets can only be either 0 or 1/√6.
Essentially, the problem is this: What is the maximum distance between a main diagonal and a face diagonal of a unit cube?