Problem
Let f: [0, 1] → [0, 1] be the function defined by f(x) = x³/3 – x² + 5x/9 + 17/36. Consider the square region S = [0, 1] x [0, 1]. Let G = {(x, y) ∈ S : y > f(x)} be called the green region and R = {(x, y) ∈ S: y < f(x)} be called the red region. Let Lh = {(x, h) ∈ S : x ∈ [0, 1]} be the horizontal line drawn at a height h ∈ [0, 1]. Then which of the following statements is (are) true?
A There exists an h ∈ [1/4, 2/3] such that the area of the green region above the line Lh equals the area of the green region below the line Lh.
B There exists an h ∈ [1/4, 2/3] such that the area of the red region above the line Lh equals the area of the red region below the line Lh.
C There exists an h ∈ [1/4, 2/3] such that the area of the green region above the line Lh equals the area of the red region below the line Lh.
D There exists an h ∈ [1/4, 2/3] such that the area of the red region above the line Lh equals the area of the green region below the line Lh.
Solution
We’ll begin by graphing the function and the two colored regions. Then, we’ll vary the line Lh and figure out which of the options are true. We’ll of course focus only on the region S.
Here’s the graph of f(x), a cubic function, which is fairly easy to plot.

Next, let’s mark the green and red regions, which are the areas within the square, that lie above and below the curve respectively.

Finally, here’s the line Lh.
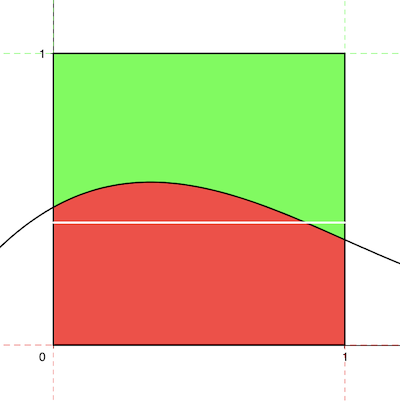
Now, in each option, h is restricted to the interval [1/4, 2/3]. So, Lh would be restricted as well.
In the applet below, drag the slider to move the line Lh and spend some time thinking about the options, before moving forward.
Of course, we’ll need some more info to figure out if the options are true. Particularly, the areas of the green and red regions, and area between the two segments and the curve.
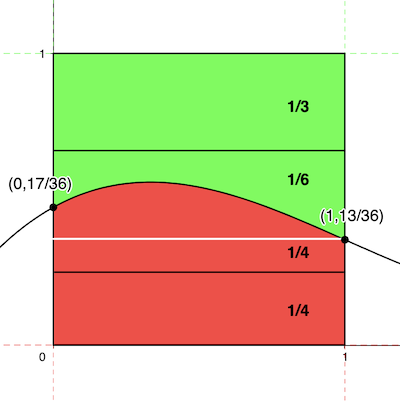
To find the area of the red region, we’ll integrate f(x) from 0 to 1. This gives a value of 1/2. That means, the green area is 1/2 as well, since they together must add up to the square’s area, which is 1.
Next, let’s find the green area between the curve and top segment (where h = 2/3). This equals 2/3 – 1/2 or 1/6.
Now, time for the red area between the curve and bottom segment (where h = 1/4). This equals 1/2 – 1/4 or 1/4.
Finally, the green rectangle at the top has the area 1 – 2/3 or 1/3. And, the red rectangle at the bottom has the area 1/4.
Let’s label the previous figure with these values.
All the groundwork has been done. We’re ready for the options.
Option A
For this option to be true, the white segment, while staying between the two black segments, must be able to divide the green region into two equal parts.
Note that if you move the white segment to the top, i.e. maximize h, the green region gets divided into areas 1/3 and 1/6.
For it to be divided equally, i.e. into areas 1/4 and 1/4, the white segment must move further upwards. But that’s not possible, since we’ve reached the maximum value of h.
So, this option is false.
Option B
For this option to be true, the white segment, while staying between the two black segments, must be able to divide the red region into two equal parts.
This can be done if you move the segment all the way to the bottom, i.e. for h = 1/4.
So, this option is true.
Option C
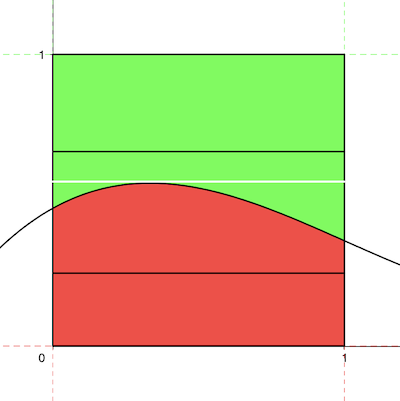
Let’s move the white segment to a point where the green area above it is the maximum, i.e. 1/2.
Here, the value of h is 13/36, and the red area below the segment is also 13/36.
Now, as we move the segment upwards, the red area below the segment increases continuously from 13/36 to 1/2 (where the segment becomes a tangent to the curve).
On the other hand, the green area above the segment decreases continuously from 1/2 to 143/324. Wait, where did that strange value come from?
The point of maximum of the function is (1/3, 181/324). And, the area of the green region above the tangent line will be 1 – 181/324 or 143/324.
So, somewhere in between, the two areas must be equal. That’s kind of the intermediate value theorem.
If we denote the red area below as R–, and the green above as G+, then R–(h) – G+(h) is negative for h = 13/36 and positive for h = 181/324.
Since the function R–(h) – G+(h) is continuous, somewhere in between, its value must be equal to zero. In other words, R–(h) = G+(h) for some value between h = 13/36 and h = 181/324.
So, this option is true.
Option D
This time, let’s move the white segment to a point where the red area below it is the maximum, i.e. 1/2.
Here, the value of h is 181/324, and the green area below the segment equal 181/324 – 1/2 or 19/324.
If we denote the red area above the segment as R+, and the green below it as G–, then R+(h) – G–(h) is negative for h = 181/324 and positive for h = 13/36.
Again, since the function R+(h) – G–(h) is continuous, somewhere in between, its value must be equal to zero. In other words, R+(h) = G–(h) for some value between h = 13/36 and h = 181/324.
So, this option is true as well.
Comments
Nice problem – truly representative of the JEE Advanced. But, painful calculations! A simpler function, like a quadratic, with integral values at the various points would’ve been nicer. Also, could’ve been worth more marks, by being posed in a paragraph style format.