Problem
Let P be the plane √3x + 2y + 3z = 16 and let S = {αi + βj + γk: α² + β² + γ² = 1 and the distance of (α, β, γ) from the plane P is 7/2}. Let u, v, and w be three distinct vectors in S such that |u – v| = |v – w| = |w – u|. Let V be the volume of the parallelepiped determined by vectors u, v, and w. Then find the value of 80V/√3.
Solution
To find the volume V, we need the scalar triple product [u v w], i.e. u.(v x w). One way in which we can get this is to find each of the vectors, if possible, using the given conditions.
Alternatively, we can use the fact that [u v w]2 = \( \begin{vmatrix} \mathbf{u}.\mathbf{u} & \mathbf{u}.\mathbf{v} & \mathbf{u}.\mathbf{w} \\ \mathbf{v}.\mathbf{u} & \mathbf{v}.\mathbf{v} & \mathbf{v}.\mathbf{w} \\ \mathbf{w}.\mathbf{u} & \mathbf{w}.\mathbf{v} & \mathbf{w}.\mathbf{w} \\ \end{vmatrix} \)
If we can find out each of the dot products, then we can take the square root of the determinant to get the answer.
Another way is to find out the volume geometrically, without using any vector formulae.
Before that, let’s dissect the problem, and understand what each given condition means. We’ll start with S.
The condition α² + β² + γ² = 1 implies that the point (α, β, γ) lies on a sphere centered at origin and of radius 1. Let’s call this sphere S.

Next, if the distance of (α, β, γ) from the given plane is fixed, then point can lie anywhere on a parallel plane at a distance of 7/2 from the given plane. Let’s call this parallel plane as P’ (the blue one below).
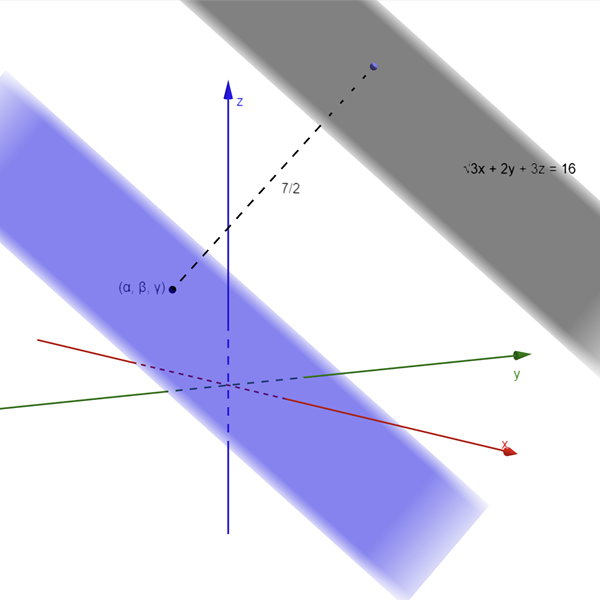
To satisfy both these conditions, (α, β, γ) must lie the intersection of the sphere S and the plane P’, which is a circle.

Finally, the condition |u – v| = |v – w| = |w – u| implies that the three points whose position vectors are u, v, and w are equidistant from each other. That is, they are the vertices of an equilateral triangle.
Lot’s going on here – please rotate the view above (click and drag) to make sure you understand everything.
In conclusion, the three points (represented by u, v, and w) are the vertices of an equilateral triangle, lying on the circle of intersection of the sphere S and the plane P’.
Now, can we find these three points? Are they unique? No.
Because, the triangle can keep rotating about the center of the circle and the above conditions will still hold. Take a look.
But even though the points are variable, the volume of the parallelopiped formed by them will remain constant.
This is because the volume depends only on the magnitudes of these vectors and the angles between them.
If you rotate the whole system about the origin, the parallelopiped also rotates, but its volume remains the same. Here’s the parallelopiped, in all its glory.
Now, we’ll dive into the two methods that I mentioned at the beginning, starting with the geometry one.
Method 1
To find the volume of the parallelopiped, we’ll find the volume of the tetrahedron formed by the same vectors, and multiply that by 6.
For the tetrahedron’s volume, we need the area of its base along with its height.
Now, the height is the perpendicular distance of the base from the vertex, i.e. the plane P’ from the origin.
This equals the distance of the plane P from the origin, minus 7/2, the distance between the two planes.
The distance of the plane P from the origin equals |√3(0) + 2(0) + 3(0) – 16|/|√(3 + 4 + 9), which comes out to be 4.
So the distance of P’ from the origin, or the height of the tetrahedron equals 4 – 7/2 or 1/2. Great!
Now, we need the area of its base, for which we need the side length of the equilateral triangle.
Let’s drop a perpendicular from the origin to the base of the tetradron, and join the foot of the perpendicular to one of the vertices of the base.

Using the Pythagorean theorem, we’ll get the unknown length in the above figure as √3/2. Now, let’s look at the base.

Using simple trigonometry, we’ll get the length of the side as 2 x (√3/2 x cos30°) or 3/2.
So, the volume of the tetrahedron equals 1/3 x area of base x height or 1/3 x √3/4 x (3/2)2 x 1/2, which equals 3√3/32.
And, the volume of the parallelopiped or V equals 6 times this volume, i.e. 9√3/16.
Finally, 80V/√3 equals 80/√3 x 9√3/16 or 45. Woohoo!
Method 2
As discussed above, we cannot find the vectors u, v, and w uniquely. So, we’ll use the alternate approach.
That is, [u v w]2 = \( \begin{vmatrix} \mathbf{u}.\mathbf{u} & \mathbf{u}.\mathbf{v} & \mathbf{u}.\mathbf{w} \\ \mathbf{v}.\mathbf{u} & \mathbf{v}.\mathbf{v} & \mathbf{v}.\mathbf{w} \\ \mathbf{w}.\mathbf{u} & \mathbf{w}.\mathbf{v} & \mathbf{w}.\mathbf{w} \\ \end{vmatrix} \)
The diagonal entries are 1 each.
And, using the condition |u – v| = |v – w| = |w – u|, we’ll get u.v = v.w = w.u. Try squaring each expression.
Since u.v = |u||v|cosθ or simply cosθ, since they’re unit vectors, all we need is to find the value of cosθ.
So, we’ll get [u v w]2 = \( \begin{vmatrix} 1 & \cosθ & \cosθ \\ \cosθ & 1 & \cosθ \\ \cosθ & \cosθ & 1 \\ \end{vmatrix} \)
Now, let’s take a look at one of the faces of the tetrahedron.
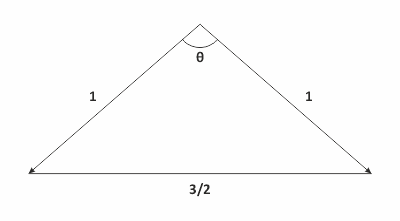
The base is the length of the side of the equilateral triangle, which we already found in the previous part.
The two equal sides are of unit length, i.e. equal to the length of the vectors u and v.
Now, we simply need to apply the cosine rule. We’ll get cosθ = (12 + 12 – (3/2)2)/(2.1.1) or -1/8.
So, [u v w]2 = \( \begin{vmatrix} 1 & \frac{-1}{8} & \frac{-1}{8} \\ \frac{-1}{8} & 1 & \frac{-1}{8} \\ \frac{-1}{8} & \frac{-1}{8} & 1 \\ \end{vmatrix} \).
Using R1 → R1 – R2 and R2 → R2 – R3, we get [u v w]2 = \( \begin{vmatrix} \frac{9}{8} & \frac{-9}{8} & 0 \\ 0 & \frac{9}{8} & \frac{-9}{8} \\ \frac{-1}{8} & \frac{-1}{8} & 1 \\ \end{vmatrix} \)
On simplifying, we get [u v w]2 = \( \frac{81}{64}\begin{vmatrix} 1 & -1 & 0 \\ 0 & 1 & -1 \\ \frac{-1}{8} & \frac{-1}{8} & 1 \\ \end{vmatrix} = \frac{243}{256}\)
Finally, we’ll get [u v w] or V = 9√3/16, which means 80V/√3 = 45.
Comments
This problem reminded me of the good old subjective format of the JEE. The kind of reasoning and calculations involved to solve this problem is truly representative of a typical 6-mark problem during those days. That said, this problem deserved more value in terms of marks, and should’ve been posed as a multi-part paragraph style problem.
\(\)