Problem
Match the following.
| List-1 | List-2 |
| (I) {x ∈ [−2π/3, 2π/3]: cosx + sinx = 1} | (P) has two elements |
| (II) {x ∈ [−5π/18, 5π/18]: √3tan3x = 1} | (Q) has three elements |
| (III) {x ∈ [−6π/5, 6π/5]: 2cos2x = √3} | (R) has four elements |
| (IV) {x ∈ [−7π/4, 7π/4]: sinx – cosx = 1} | (S) has five elements |
| (T) has six elements |
Solution
Since we need to find the number of solutions, we’ll plot the graphs of each function on the LHS, and find the number of points of intersection with the respective graphs for the RHS.
Let’s do that for each equation one by one.
Option I
On dividing both sides by √2, the given equation converts to cos(π/4 – x) = 1/√2.
Here’s what the graph looks like:

In the given interval, the equation has two solutions. So, (I) matches with (P).
Option II
The equation can be rewritten as tan3x = 1/√3. Here’s what the graph looks like:

In the given interval, the equation has two solutions. So, (II) matches with (P) as well.
Option III
The equation can be rewritten as cos2x = √3/2. Here’s what the graph looks like:

In the given interval, the equation has six solutions. So, (III) matches with (T).
Option IV
On dividing both sides by √2, the given equation converts to cos(π/4 + x) = -1/√2.
Here’s what the graph looks like:
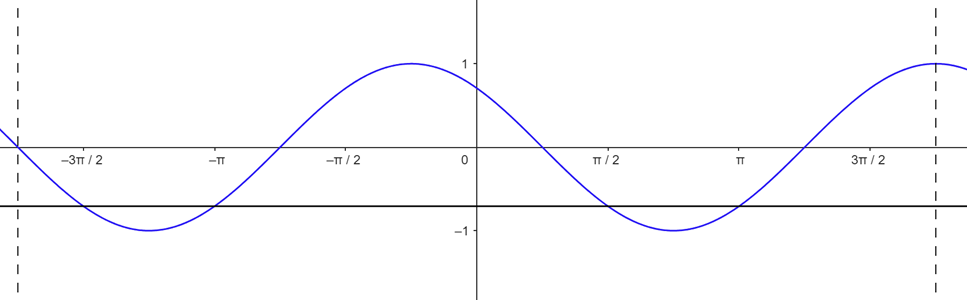
In the given interval, the equation has four solutions. So, (IV) matches with (R).
Comments
A direct problem based on trigonometric equations – pretty straightforward (and boring). More like a JEE Main problem.