In this lesson, we’ll derive the slope-intercept form of the line, taking different orientations of the same. This is something that I discussed in the previous lesson.
Case 1
We’ll start by taking P(x, y) in the second quadrant.

We’ve also constructed PA parallel to the Y-axis and PB parallel to the X axis.
Now,
OB = PA = y
BC = OC – OB = c – y
Also,
PB = -x
Now, let’s try to relate the coordinates of P with the given slope and intercept. In ΔPBC, we have:
tanθ = CB/PB = (c – y)/(-x)
And, that’s all. On rearranging, we’ll get:
y = (tanθ)x + c
or
y = mx + c
We got the same equation. Nice!
Case 2
Let’s try taking P(x, y) in the third quadrant.
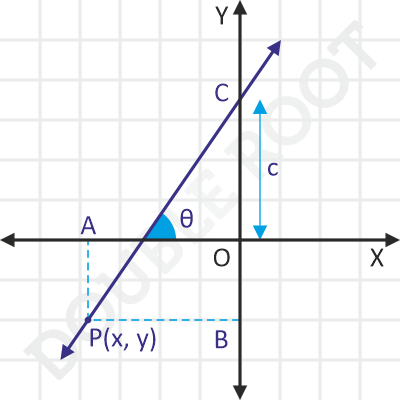
Again, we’ve constructed PA parallel to the Y-axis and PB parallel to the X axis.
In this case,
OB = PA = -y
BC = OC + OB = c + (-y)
Also,
PB = -x
Now, let’s try to relate the coordinates of P with the given slope and intercept. In ΔPBC, we have:
tanθ = CB/PB = (c – y)/(-x)
And, on rearranging, we’ll get:
y = (tanθ)x + c
or
y = mx + c
Same equation! Still not convinced? Let’s take another case.
Case 3
This time, we’ll take a line that makes an obtuse angle with the X-axis.

Once again, we’ve constructed PA parallel to the Y-axis and PB parallel to the X axis.
Now,
OB = PA = -y
CB = OC + OB = c + (-y)
Also,
PB = x
Now, let’s try to relate the coordinates of P with the given slope and intercept. In ΔPBC, we have:
tan(π – θ) = CB/PB = (c – y)/x
And, on rearranging, we’ll get:
y = (tanθ)x + c
or
y = mx + c
Same. Equation. I know you’re convinced now. Still, why don’t you try taking some more orientations of the line and different positions of P on it? You should get the same equation in each case.
I’ll end this lesson now. The next one will discuss a few examples related to the slope-intercept form. See you there!