In this lesson, we’ll discuss a few more examples on the parametric form of the equation of a straight line. In case you haven’t gone through the previous lesson, please do that before proceeding with this one.
Example 4 A square has end points of its diagonals as A(1, -1) and C(0, 4). Find the coordinates of the other two vertices.
Solution Here’s a figure that shows what we need.

Let’s look at three different methods.
Method I
If we assume the coordinates of B as (x, y), then these coordinates must satisfy the following equations:
AB = BC (since the sides are equal)
AB2 + BC2 = AC2 (since the sides are perpendicular)
In fact, these equations will give the coordinates of D as well, since they too satisfy the same equations.
You can proceed from here yourself. The distance formula might come in handy.
Method II
Here’s the previous figure.
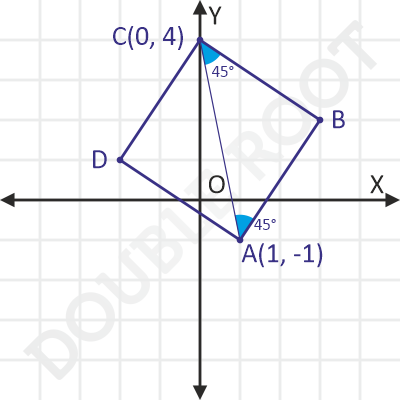
The sides AB and AD, both make an angle of 45° with the diagonal AC. This situation is similar to Example 4 in this lesson. I’ll skip the details here.
Using the same method as in the example, we can get the equations the sides:
AB: y + 1 = (-2/3)(x – 1)
AD: y + 1 = (3/2)(x – 1)
CB: y – 4 = (3/2)(x – 0)
CD: y – 4 = (-2/3)(x – 0)
Solving the first and third equations will give the coordinates of B, which are (-2, 1).
Similarly, solving the second and fourth equations will give the coordinates of D, which are (3, 2).
This is quite a long method, and so was the first method. A much shorter one involves the parametric equation, which is up next!
Method III
Let AC and BD intersect at P.
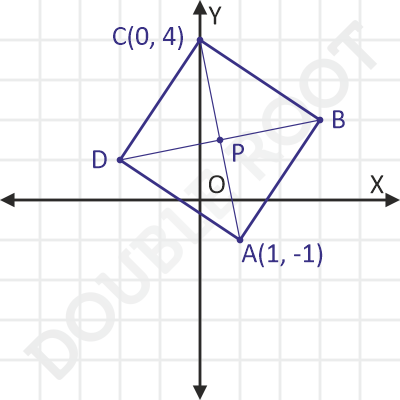
We have to find the coordinates of points (i.e. B and D), that are at some distance from the point P. That means, we can find the coordinates of these points by using the parametric equation of BD.
For that, we’ll need three things:
The coordinates of P (i.e. (x1, y1))
The slope of BD (i.e. tanθ)
The distances PB and PD (i.e. r)
We can find each of these easily:
P = (1/2, 3/2) (using the midpoint formula)
PB = PD = √26/2 (i.e. half of AC, which can be found using the distance formula)
Slope of BD = 1/5 (since it is perpendicular to AC, whose slope is -5)
Using the slope, we’ll get
sinθ = 1/√26
cosθ = 5/√26
Here, θ is the angle made by BD with the positive X-axis.
Finally, the parametric equation of the line BD is:
(x – 1/2)/cosθ = (y -3/2)/sinθ = r
Putting r = ±√26/2, we get the required coordinates straight away as (3, 2) and (-2, 1). Almost effortless!
Example 5 A line, which passes through P(x1, y1) and whose slope is tanθ, meets the line ax + by + c = 0 at A. Find the distance PA.
Solution This is what we’re looking for.

Let’s discuss two different methods.
Method I
We’ll start by find the equation of the line, using the point slope form:
(y – y1) = tanθ(x – x1)
Next, we’ll solve this equation with ax + by + c = 0, to get the coordinates of A.
Finally, we’ll use the distance formula to find PA. This will get quite ugly. So, I’ll stop here.
Method II
Here’s the previous figure.

Let’s assume PA to be r. Then, using the parametric equation of the line PA, the coordinates of A are:
(x1 + rcosθ, y1 + rsinθ)
Since A also lies on the other line ax + by + c = 0, we have:
a(x1 + rcosθ) + b(y1 + rsinθ) + c = 0
On solving this for r, we’ll get:
r = |ax1 + by1 + c|/(acosθ + bsinθ) (the absolute value takes care of negative values)
Once again, the parametric equation saved the day!
In case you didn’t notice, the final expression looks a bit familiar to perpendicular distance of P from the line, that is:
d = |ax1 + by1 + c|/√(a2 + b2)
Are these two connected in some way?
Turns out they are. The expression for r is the distance P from the line in a given direction. What if this direction is perpendicular to the line? In that case,
tanθ = b/a
⇒ sinθ = b/√(a2 + b2)
⇒ cosθ = a/√(a2 + b2)
Now, you can substitute these values in the expression for r and see if you get the same one as d.
I’ll stop here. Hope you have an idea when to use the parametric form, instead of other forms of the equations. And I also hope that you have begun to appreciate its usefulness, and understand its power!
Next, I’ll talk about the relative position of two points with respect to a line.