Hi. This lesson covers a few examples of the parametric form of the equation of a straight line.
Example 1 Find the coordinates of the points on the line 3x – 4y + 1 = 0 at a distance of 5 units from the point A(1, 1).
Solution First, let me illustrate a method of finding out the required coordinates without using the parametric form.
If the coordinates of the required point be (x1, y1), then since the point
- lies on the given line, we have 3x1 – 4y1 + 1 = 0.
- is at a distance 5 units from (1, 1), we have (x1 – 1)2 + (y1 – 1)2 = 25.
Substituting the value of x1 from the first equation in the second, we’ll get two values of y1, 4 and -2. Using these, we get the corresponding values of x1 as 5 and -3.
Therefore, we have two points which satisfy the given conditions: (5, 4) and (-3, -2).
Here’s another method.
Since the point A lies on the given line, we can use the parametric form of its equation.
The slope of the line (tanθ) is 4/3. This makes cosθ = 3/5, and sinθ = 4/5. We’ll get the parametric equation as:
(x – 1)/(3/5) = (y – 1)/(4/5) = r
This means that any point on this line has the coordinates (1 + 3r/5, 1 + 4r/5), where r denotes the distance of the point from (1, 1).
Now, what we want is the coordinates of the points at a distance of 5 units from the point (1, 1).
So, we’ll simply substitute r = ±5 in the previous coordinates, and we get the two points effortlessly as (1 + 3, 1 + 4) and (1 – 3, 1 – 4) or (5, 4) and (-3, -2) respectively.
Here is a figure to illustrate the situation.

Example 2 Find the coordinates of the point on the line 2x + y = 2, which lies at a distance of 1 unit from the origin.
Solution This is a similar problem. The difference here is that the point, from which the distance is given, does not lie on the given line.
We can still use the parametric equation. Let’s see how.
Suppose we draw a line L passing through the origin, that intersects the given line at A.
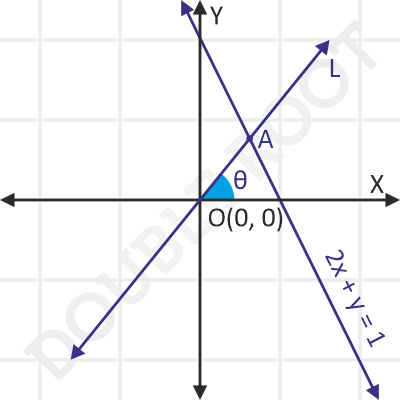
The parametric equation of the line L is:
x = 0 + rcosθ
y = 0 + rsinθ
Here, r is the distance of the point (x, y) from (0, 0).
We are interested in the particular point where r = 1. Plus, the point should lie on the line 2x + y = 2.
Putting r = 1, and substituting the resulting coordinates in the equation 2x + y = 2, we’ll get:
2cosθ + sinθ = 2
This gives two values of θ, 0 and arctan(4/3). Geometrically, this means there will be two such points on the given line.
Finally, the required coordinates will be obtained by substituting the values of θ (and r) in the above parametric equation. These coordinates are:
(1, 0) and (4/5, 3/5)
You could’ve the distance formula here as well. Please try that yourself and compare the two solutions to get an idea about which one is more efficient.
Example 3 In what direction must the line passing through A(1, 2) be drawn, so that its point of intersection with the line x + y = 4, is at a distance 1/√2 units from A?
Solution Here’s a figure that illustrates the problem.
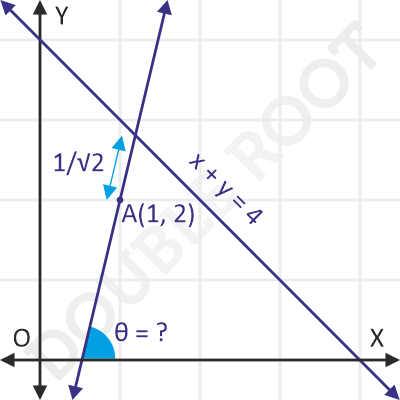
We need to find the value of θ (i.e., the direction) for which PQ = 1/√2. To find that we’ll use the parametric equation of this line:
(x – 1)/cosθ = (y – 2)/sinθ = r
Putting r = 1/√2, and substituting the coordinates in the given line, we’ll get:
cosθ + sinθ = √2
This gives the value of θ as 45°. That’s all!
I’ll stop here and continue with a few more examples in the next lesson.