Time for examples involving the normal form of the equation to a straight line.
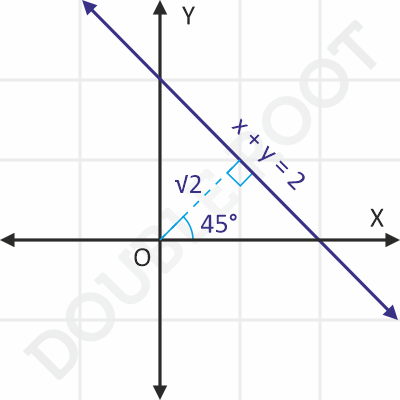
Example 1 Find the equation of a line whose perpendicular distance from the origin is √2, and the perpendicular to it from the origin makes a 45° angle with the x-axis.
Solution To find the equation, we’ll use the above form directly.
⇒ xcos45° + ysin45° = √2
⇒ x/√2 + y/√2 = √2
⇒ x + y = 2
The figure shows the line on the XY plane.
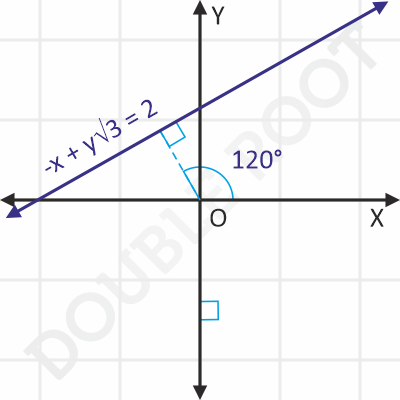
Example 2 Find the equation of a line whose perpendicular distance from the origin is 1, and the perpendicular to it from the origin makes a 120° angle with the x-axis.
Solution To find the equation, we’ll use the above form directly.
xcos120° + ysin120° = 1
⇒ -x/2 + y√3/2 = 1
⇒ -x + y√3 = 2
The figure shows the line on the XY plane.
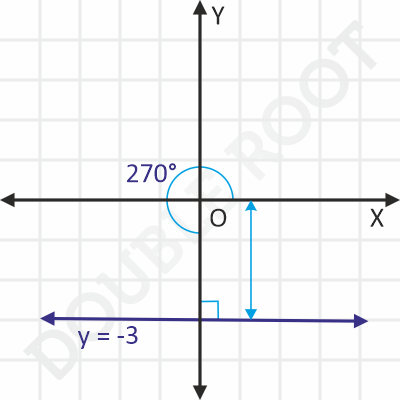
Example 3 Find the equation of a line whose perpendicular distance from the origin is 3, and the perpendicular to it from the origin makes a 270° angle with the x-axis.
Solution To find the equation, we’ll use the above form directly.
⇒ xcos270° + ysin270° = 3
⇒ 0x – y = 3
⇒ y = -3
The figure shows the line on the XY plane.
That’s it for this lesson. We’ll come back to normal form later (possibly in a lesson on conic sections).
The next lesson will talk about the general form of the equation of a straight line.