This lesson will cover another form of the equation of a straight line, called the normal form.
This form is less frequently used as compared to the previous ones. You wouldn’t see it around much. Still, let’s take a look.
In this case, the length of the perpendicular from origin to the line is equals p, and this perpendicular makes an angle θ with the X-axis.
Confused? Here’s what I mean.

To derive the equation, we’ll use the intercept form of the equation of a line.
Using some trigonometry, we can find the intercepts of this line in terms of p and θ.
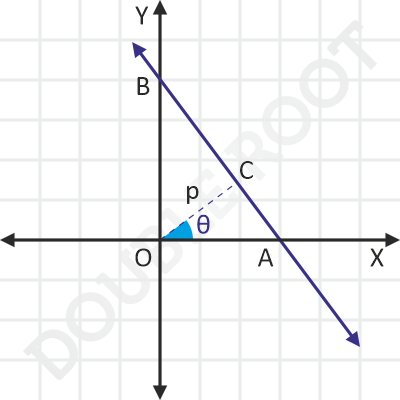
In ΔOAC,
cosθ = OC/OA
⇒ cosθ = p/OA
⇒ OA = psecθ
In ΔOBC,
cos(90° – θ) = OC/OB
⇒ sinθ = p/OB
⇒ OB = pcscθ
We’ve found the intercepts! Let’s use the intercept form of the equation now. We’ll get the equation as:
x/psecθ + y/pcscθ = 1
This gives us the following:
xcosθ + ysinθ = p
This form is known as the normal form of the equation of a line. And here’s a simulation that let’s you play with it.
Try changing the values of θ and p, and observe how the line changes.
That’s all about the normal form. Keep it handy. You’ll need it one day.
Lesson Summary
- The equation of the line, whose perpendicular distance from origin is p, and this perpendicular makes an angle θ with the X-axis, is given by xcosθ + ysinθ = p.
That’s all. See you in the next lesson with some examples.