1. Introduction

Welcome to the first lesson in the straight line series!

Over the next few (read: many) lessons, I’ll be covering the various forms of equations of a straight line, and a lot of related concepts, formulas, and applications.

Let’s get started!

To find the equation to a straight line, we’ll take a random point P(x, y) on the line, and find the relation between the coordinates, which will always hold true. This relation is the definition of the equation to any curve, as explained here.

We’ll start with the simple ones – lines which are parallel to one of the axes.

Equation of a Line Parallel to the X-axis

Suppose we have a line that is parallel to the x-axis and it at a distance d from it. How can we find its equation?

To do that, let’s take any point P(x, y) on this line.

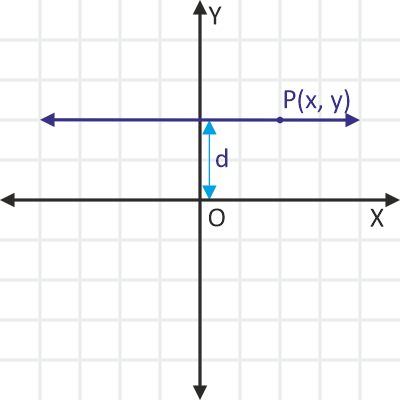
Can we find a relation involving the coordinates of P(x, y) that will always hold true?

Since the line is parallel to the X-axis, its distance from the axis always remains the same (i.e. d). That means, any point on this line will be at a distance d from the X-axis. So, the distance of P(x, y) from the X-axis will also be d.

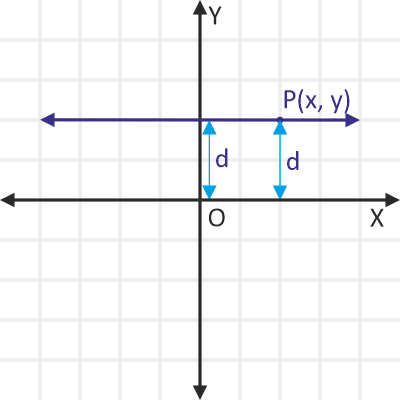
Since the (signed) distance of a point from the X-axis is its y-coordinate, we can express this relation as:

y = d

And, since this relation is always true (i.e., for any position of P on the line), this is the required equation of the line.

Here are a couple of examples.

Equation of a Line Parallel to the Y-axis

Suppose we have a line that is parallel to the Y-axis and it at a distance c from it. How can we find its equation?

We’ll use the same method as in the previous case. Let’s take any point P(x, y) on this line.

Now, we need to find a relation involving the coordinates of P(x, y) that will always hold true.

Since the line is parallel to the Y-axis, its distance from axis always remains the same (i.e. c). That means, any point on this line will be at a distance c from the X-axis. So, the distance of P(x, y) from the Y-axis will also be c.

Since the (signed) distance of a point from the Y-axis is its x-coordinate, we can express this relation as:

x = c

And, since this relation is always true (i.e., for any position of P on the line), this is the required equation of the line.

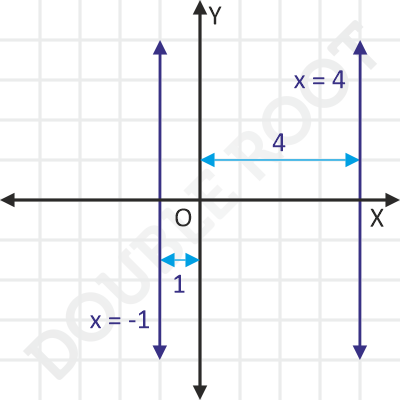
Here are a couple of examples.

Equation of the X axis and the Y axis

What about the equations of the axes themselves? Following the same method as above, the distance of the X axis from the X axis is… zero!

Therefore, its equation is y = 0. Similarly, the equation of the Y axis is x = 0.

Hope you understood how we derived the equations. Here’s a simulation where you can explore these lines.

Try dragging the two sliders and observe how the lines change. That’s all for the first lesson. See you in the next one!

Lesson Summary

1. The equation of a line parallel to the X axis will be of the form y = d, where d is the signed distance of the line from the X axis.
2. The equation of a line parallel to the Y axis will be of the form x = c, where c is the signed distance of the line from the Y axis.
3. The equation of the X axis is y = 0.
4. The equation of the Y axis is x = 0.

The next lesson will deal with the equations of lines which are not parallel to any of the axes.