This lesson will focus on examples on the intercept form of the equation of a straight line.
Example 1 Find the equation of a line whose
(i) x-intercept is -4 and y-intercept is 3.
(ii) x-intercept is 2 and y-intercept is -5.
Solution In both parts, we directly have to apply the intercept form of the equation of a line.
(i) We know that the intercept form of the equation is:
x/a + y/b = 1
Let’s plug in the given values. We’ll get:
x/(-4) + y/3 = 1
or
3x – 4y + 12 = 0
(ii) Again, we’ll plug in the values of the given intercepts into the equation. We’ll get:
x/2 + y/(-5) = 1
or
-5x + 2y + 10 = 0
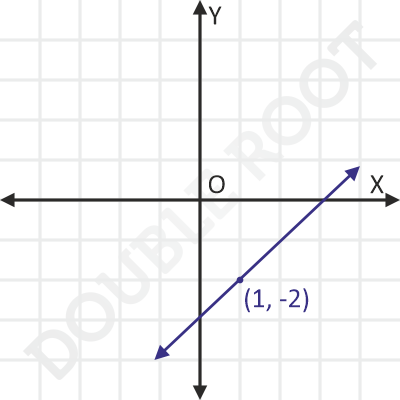
Example 2 Find the equation of the line passing through (1, -2) cutting off equal intercepts, but of opposite signs, from the axes.
Solution The information provided in the problem involves intercepts. So it will be better to start with the intercept form of the equation. Although any other form will lead to the same answer, but we should prefer efficient methods.
Alright. The equation can be assumed to be
x/a + y/b = 1
Given that, the intercepts are equal but opposite in sign. So,
a = -b
And, the line passes through the point (1, -2). So,
1/a + (-2)/b = 1
Solving the previous two equations, we get:
a = 3
b = -3
Therefore, the required equation is:
x/3 + y/(-3) = 1
or
x – y = 3
The line would look something like this.
Example 3 A line intersects the X-axis and the Y-axis at the points A and B respectively. It also passes through a point C(4, 3) which divides AB in the ratio 1 : 2 internally. Find the equation of the line.
Solution This is how the line would look like.
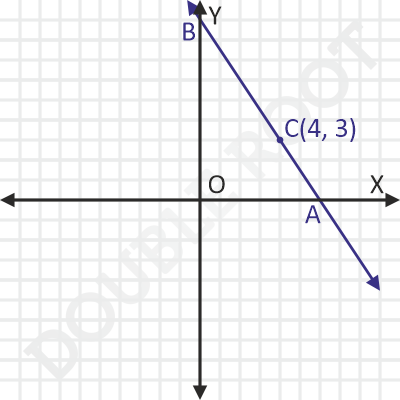
Let’s’ assume the equation of the line to be:
x/a + y/b = 1
This means that the coordinates of A and B are be (a, 0) and (0, b) respectively.
Since C divides AB in the ratio 1 : 2 internally, we can apply the section formula to relate the coordinate of the three points. We’ll get:
4 = (1 x 0 + 2 x a)/(1 + 2)
3 = (1 x b + 2 x 0)/(1 + 2)
The first equation gives a = 6 and the second one gives b = 9. And we’re done! The required equation is:
x/6 + y/9 = 1
Example 3 Find the equation to the line, sum of whose intercepts is 10 and
(i) makes equal angles with the axes.
(ii) makes a triangle of area 12 with the axes.
Solution We can assume the equation to be:
x/a + y/b = 1
In both parts, we have:
a + b = 10
(i) If the line makes equal angles with the axes, then the intercepts must be equal in magnitude, though they could be of same or opposite signs. Take a look.

For example, in triangle OAB, the equal angles OAB and OBA (each measuring 45o) make the sides opposite to them (i.e., the intercepts) also equal.
What does that mean? Either a = b, or a = -b. But the latter would mean a + b = 0, which violates the other condition (i.e. a + b = 10).
Thus, a = b is the only possibility. And using alongwith the other condition, i.e. a + b = 10, we’ll get both a and b as 5.
Therefore, the required equation becomes:
x/5 + y/5 = 1
or
x + y = 5
(ii) The area of the triangle formed with the axes in terms of the intercepts a and b will be |1/2 ab|. The following figure explains it.
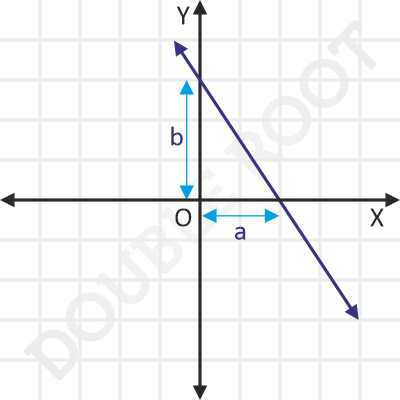
The absolute value takes care of the negative intercepts.
Using the given information we have,
|1/2 ab| = 12
⇒ |ab| = 24
Also,
a + b = 10
Solving these two equations, we get four sets of solutions:
a = 6, b = 4
a = 4, b = 6
a = 12, b = -2
a = -2, b = 12
We therefore get four possible lines:
x/6 + y/4 = 1
x/12 + y/(-2) = 1
x/4 + y/6 = 1
x/(-2) + y/12 = 1
That’s all for this lesson. Keep in mind that the problems could be solved using a different form of the equation as well. As you solve more problems, you’ll get a better idea of which equations will provide a good starting point.
In the next lesson, I’ll discuss another form of a line’s equation, known as the point-slope form.