In this lesson, we’ll derive the intercept form of the straight line.
Suppose there’s a line whose x-intercept is a and y-intercept is b. That is, the line passes through point on the x-axis a units from the origin, and also passes through a point on the y-axis b units from the origin.
Have a look.
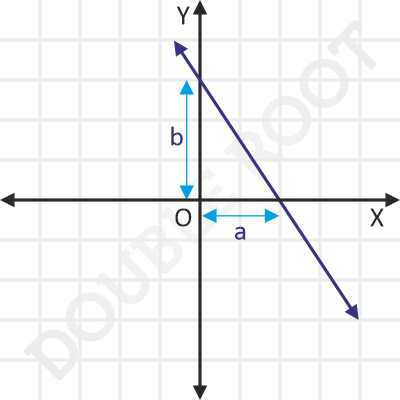
How can we find its equation? Let’s look at two different methods for the same.
Method I
We already know one method of finding the equation of a line, given its slope and y-intercept. The y-intercept is b. So the equation must look like y = mx + b.
What about m? Recall that m equals tanθ, where θ is the angle that the line makes with the X axis. Can we relate tanθ to a and b?
Here’s the figure again.
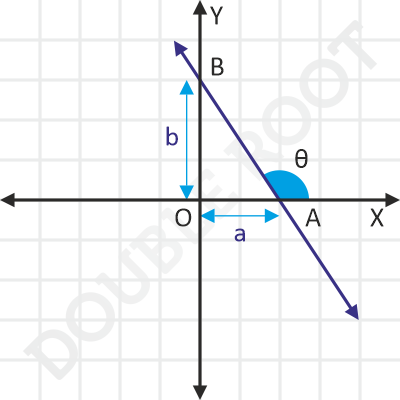
In triangle OAB, we have:
tan(π-θ) = OB/OA = b/a
⇒ -tanθ = b/a
⇒ m = -b/a
And we’re done. The required equation is
y = -(b/a)x+b,
This can be rearranged to get a better looking equation
x/a + y/b = 1
This is the intercept form of the equation of a line. Let’s look at the next method.
Method II
The previous method used the slope-intercept form of a line’s equation. Suppose we didn’t know about that form.
Then, to find the equation, we’ll take a random point P(x, y) on the line, and find a relation between its coordinates that always holds true.
Let’s join P to O.
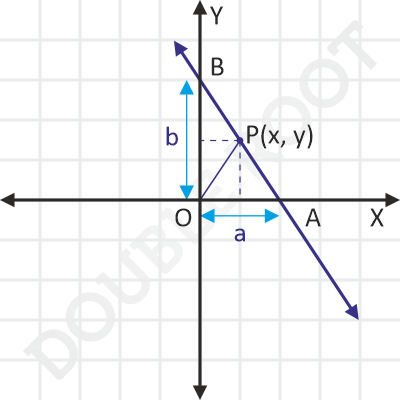
Then, we can express the area of ΔOAB in terms of the areas of ΔPOA and ΔPOB.
We have:
Ar(OAB) = Ar(OAP) + Ar(OPB)
That is,
1/2 . a . b = 1/2 . a . y + 1/2 . b . x
After rearranging the terms, we get the same equation as above:
x/a + y/b = 1
Here’s a simulation where you can observe the intercept form of the line. Try changing the intercepts and see how the line changes.
Lesson Summary
- The equation of the line, which makes intercepts of a and b on the X and Y axis respectively, is given by x/a + y/b = 1.
- The points of intersection of this line with the X and Y axis are (a, 0) and (0, b) respectively.
Try deriving the equation by taking P in the 2nd quadrant. You should get the same equation. Take care of the signs of a, b, x and y.
The next lesson will cover a few examples to illustrate the intercept form of the line. See you there!