22. Distance of a Point From a Line: Examples

Hi. This lesson will cover a few examples related to the distance of a point from a line.

Example 1 Find the distance of the point P(2, 3) from the line 4y = 3x + 1.

Solution Here’s a figure to illustrate the problem.

To find the distance, we can directly apply the formula that we derived in the previous lesson. Before that, we’ll have to transform the equation so that all terms are on the same side. We’ll get:

3x – 4y + 1 = 0

Now, using the formula, we’ll get the required distance as:

|3(2) – 4(3) + 1| / √(3² + (-4)²)

= |-5| / √25

= 1

 

Example 2 The line 12x + 5y + 9 = 0 is tangent to a circle whose center lies at C(1, 1). Find the area of the circle.

Solution To find the area, we need the circle’s radius. How can we find that using the given information? Take a look at the figure.

The radius is perpendicular to the tangent at its point of contact. That means, to find the radius, we need to find the perpendicular distance of the tangent from the center of the circle:

r = |12(1) + 5(1) + 9| / √(12² + 5²)

= 2

We can now calculate the area of the circle, which equal 4π square units.

 

Example 3 Show that any point on the line 7x + 9y = 0 is equidistant from the lines 3x – 4y + 5 = 0 and 12x – 5y + 13 = 0.

Solution Here’s a simulation that illustrates the problem.

Try dragging the point P. Is PA always equal to PB? How can we prove that?

We’ll begin by taking any point P(x₁, y₁) on the line 7x + 9y = 0.

Then, let’s find the distances which we need to prove as equal. These are:

|3x₁ – 4y₁ + 5|/5

|12x₁ – 5y₁ + 13|/13

Skipped some calculations there. Are the two expressions (or distances) equal? They don’t look equation, yet.

Because, we haven’t used the fact that the point (x₁, y₁) lies on the line 7x + 9y = 0. That is,

7x₁ + 9y₁ = 0 or x₁ = -9y₁/7

Now, let’s substitute this value of x₁ in the previous expressions. The first one becomes:

|3(-9y₁/7) – 4y₁ + 5|/5

= |-11y₁ + 1|

The second once becomes:

|12x₁ – 5y₁ + 13|/13

= |12(-9y₁/7) – 5y₁ + 13|/13

= |-11y₁ + 1|

Now, the two distances look equal. Nice.

P.S. The line 7x + 9y = 0 bisects the angle between the other two lines. Only then will it be possible for any point on this line to be equidistant from the other two. I’ll talk about angle bisectors later.

 

Example 4 Find the area of the isosceles right angled triangle whose base has the equation 3x – y = 2 and the opposite vertex lies at (1, -3).

Solution Here’s a figure that shows the triangle. It’s always a good practice to draw a figure representing the problem.

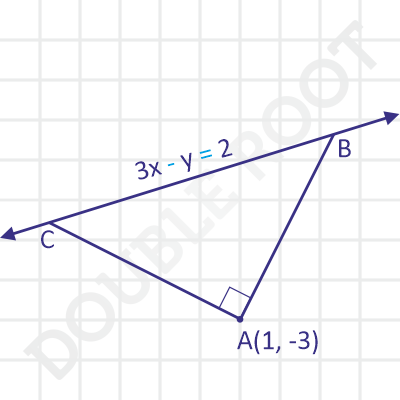
To find the area, we’ll find the altitude AD from A, and then find the base BC. Finally, we’ll use the area formula.

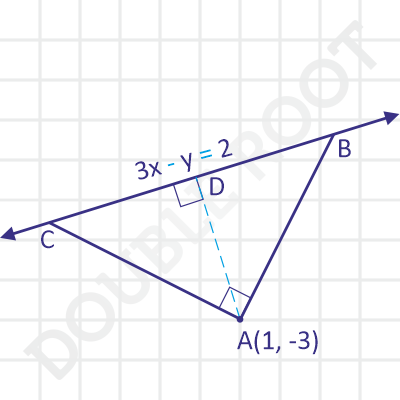
Now, the altitude is the perpendicular distance of the base 3x – y = 2 from the vertex (1, -3), which is:

|3(1) – (-3) -2| / √(3² + (-1)²)

= 4/√10

Now, since the triangle is isosceles, the angles B and C will measure 45° each. Using trigonometry in ΔADC, we’ll get:

tan45° = AD/CD

⇒ 1 = AD/CD

⇒ CD = AD

Similarly,

BD = AD

Therefore,

BC = BD + CD = 2AD = 8/√10

Therefore, the required area will be:

1/2 x BC x AD

= 1/2 x 8/√10 x 4/√10

= 8/5 sq. units

That’s all for this lesson. In the next one, we’ll use this formula to find the distance between parallel lines. See you there.