This lesson will cover a few examples related to distance of point from a line.
Example 1 Find the distance between the lines
(i) 4x + 3y = 5 and 4x + 3y = 10
(ii) y = x + 1 and 2x = 2y + 5
Solution To find the distance, we’ll apply the formula from the previous lesson, after transforming the equations as necessary.
(i) The two lines can be rewritten as
4x + 3y – 5 = 0
4x + 3y – 10 = 0
Therefore, the required distance equals:
|(-5) – (-10)| / √(42+32)
= |5| / 5
= 1
(ii) The two equations can be rewritten as:
x – y + 1 = 0
2x – 2y – 5 = 0
Before we can apply the formula, we must tranform either equation so that the corresponding coefficients of x and y are the same. We’ll do this by multiplying the first equation by 2. We’ll get:
2x – 2y + 2 = 0
Now, we can find the distance between the two lines, which equals:
|2 – (-5)| / √(22+(-2)2)
= 7/√8
Example 2 Find the equation of the lines parallel to the line 5x + 12y – 13 = 0, which are at a distance of 2 units from it.
Solution Here’s a figure that illustrates the problem.
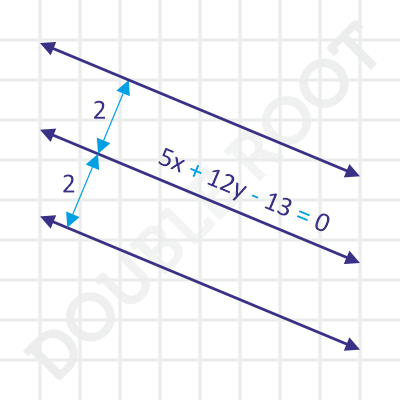
We know that any line parallel to the given line will be of the form 5x + 12y + k = 0. To find k, we’ll find the distance between this and the given line, and equate it to 2.
The distance between these two lines is
|k – (-13)| / √(52+122)
And, since this distance is given to be 2, we have:
|k – (-13)| / √(52+122) = 2
⇒ |k + 13|/13 = 2
⇒ |k + 13| = 26
⇒ k + 13 = ± 26
⇒ k = 13 or k = -39
Therefore, the required equations are:
5x + 12y + 13 = 0
5x + 12y – 39 = 0
Example 3 The equations of two sides of a square are 3x + 4y – 5 = 0 and 3x + 4y – 15 = 0. If the third side passes through (6, 5), find the equations of the remaining sides.
Solution Note that the two given lines are parallel, and therefore are equations of opposite sides. Here’s a figure to illustrate.
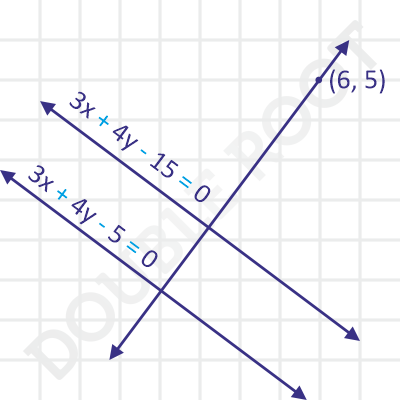
The other two sides will have equations of the form 4x – 3y + k = 0 (since they are perpendicular to the given sides).
Since one of them passes through (6, 5) we have:
4(6) – 3(5) + k = 0
⇒ k = -9
Therefore, one of the remaining sides has the equation:
4x – 3y – 9 = 0
What about the other one?
Since the equations represent sides of a square, the distance between the opposite sides will be equal.
That is, the distance between 3x + 4y – 5 = 0 and 3x + 4y – 15 = 0 will be same as the distance between 4x – 3y – 9 = 0. and the fourth side 4x – 3y + k’ = 0.
We can now proceed in a similar manner as the previous example. I’ll skip the calculations. We’ll get two values of k’, 1 and -19.
This means that there are two possible equations of the fourth side. Do you see the two possibilities in the figure above?
Finally, the possible equations of the fourth side are:
4x – 3y + 1 = 0
4x – 3y – 19 = 0
In the next lesson, we’ll take a little detour and discuss the parametric form of the equation of a straight line.