32. Angle Bisectors

In this lesson, we’ll find the equation of the lines, which bisect the angle between two given lines. That is, the equations of the angle bisectors of the two lines.

Let’s discuss two different methods.

Method 1

Let the two given lines be:

L₁: a₁x + b₁y + c₁ = 0

L₂: a₂x + b₂y + c₂ = 0

Now, the angle bisectors of L₁ and L₂ are the lines that:

pass through the point of intersection L₁ and L₂, and

make equal angles L₁ and L₂.

We’ll start by finding the point of intersection of the lines. Let’s say the point we get is (x₁, y₁).

Next, we need to find the slope m of the angle bisectors.

Since they make the same angle with L₁ and L₂, using the formula for the angle between two lines, we’ll get:

|(m – m₁)/(1 + mm₁)| = |(m – m₂)/(1 + mm₂)|

⇒ (m – m₁)/(1 + mm₁) = ±(m – m₂)/(1 + mm₂)

Here, m₁ and m₂ are the slopes of L₁ and L₂ respectively.

Solving the previous equation will give us two values of m, which means we’ll get two angle bisectors (one for each value of m).

Finally, we can find their equations using the point-slope form.

As you might have figured out, this method is quite complicated. Let’s move on the next one, which is much more elegant.

Method 2

Let’s begin with the previous two lines:

L₂: a₁x + b₁y + c₁ = 0

L₂: a₂x + b₂y + c₂ = 0

To find the equation of the angle bisectors, we’ll use some geometry – any point on the angle bisector will be equidistant from the two lines. Have a look.

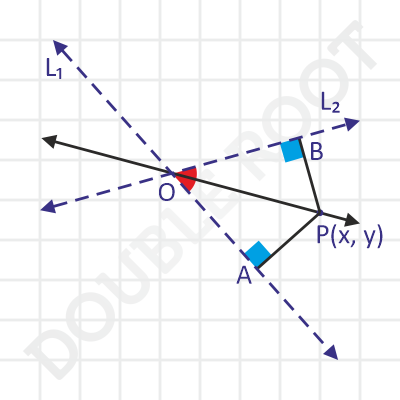
If P is any point on the angle bisector, then PA will always be equal to PB. Why? Because the two triangles POA and POB will always be congruent.

We’ve found a relation that is true for any point P on the angle bisectors. Recall that this is all we need to find the equation of the locus of P (i.e., the equation of the angle bisectors).

Now, we just need to convert this to an equation that involves the coordinates of P. Let’s assume them be (x, y). Since PA = PB, using this formula, we can write:

|a₁x + b₁y + c₁| / √(a₁² + b₁²) = |a₂x + b₂y + c₂| / √(a₂² + b₂²)

And, this is the required equation!

On removing the modulus, we get two equations (implying that we have two angle bisectors):

(a₁x + b₁y + c₁) / √(a₁² + b₁²) = (a₂x + b₂y + c₂) / √(a₂² + b₂²)

(a₁x + b₁y + c₁) / √(a₁² + b₁²) = – (a₂x + b₂y + c₂) / √(a₂² + b₂²)

Lesson Summary

1. The equation of the angle bisectors of the lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 will be given by (a₁x + b₁y + c₁)/√(a₁² + b₁²) = ± (a₂x + b₂y + c₂)/√(a₂² + b₂²)

That’s it for this lesson. Next, I’ll cover some examples related to angle bisectors. See you there!