In this lesson, I’ll illustrate a few more examples involving the formula for angle between two lines. A couple of these have already been discussed here.
Example 3 Find the orthocenter of the triangle whose vertices are A(0, 0), B(1, 2) and C(2, 1).
Solution The orthocenter (H) is the point of concurrency of the altitudes of the triangle. To find its coordinates, we’ll find the equations of any two altitudes and then their point of intersection (which is nothing but H).
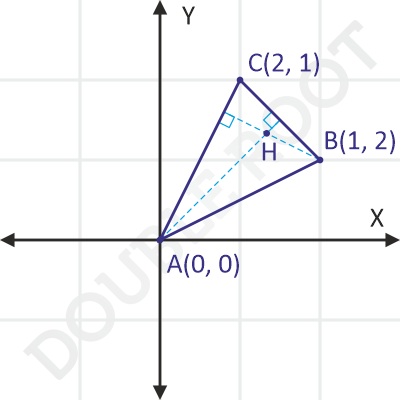
To find the equation of an altitude (say AH), we can use the following information:
The altitude passes through A
The altitude is perpendicular to the opposite side, i.e. BC
The slope BC equals:
(2 – 1)/(1 – 2) or -1
Using the condition for perpendicularity (discussed here), the slope of AH equals:
(-1)/(-1) or 1
Using the point slope form, the equation of AD is
y – 0 = 1(x – 0) or x – y = 0.
Similarly, the equation of the BH is:
2x + y – 4 = 0
Solving these two equations of the altitudes will give us the coordinates of the orthocenter, which are (4/3, 4/3).
As an exercise, try to find the coordinates of the circumcenter of this triangle (i.e. the point of concurrency of the perpendicular bisectors of the sides). The method will be quite similar.
Example 4 An isosceles right angled triangle has its hypotenuse along the line 2x + y = 4. If the opposite vertex is (3, 2), then find the equations of its sides.
Solution Here’s a figure that illustrates the situation.
Both lines pass through the point (1, 2). Is there a way to find their slopes?
Turns out there is! Since the triangle is an isosceles right angled triangle, the angles A and B both equal 45°. That means, both these lines make an angle of 45° with the given line.
So, we can find their slopes using the formula for angle between two lines. Finally, we can find their equations using the point slope form.
The slope of the given line is (-2)/1 or -2. Using the formula for angle between two lines, we’ll get:
tan45° = |(m – (-2)/(1 + m x (-2))|
⇒ 1 = |(m+2)/(1 – 2m)|
⇒ (m+2)/(1 – 2m) = ±1
Solving the above equation taking RHS as 1 and -1 separately gives m as -1/3 and 3 respectively. Note that the product of the slopes is -1, implying that the lines are perpendicular.
Finally, the equations of these lines are:
y – 2 = -1/3(x – 3)
y – 2 = 3(x – 3)
Example 5 Find the equation of the line which is perpendicular to the line 3x + 4y = 12, and intersects it at a point on the X axis.
Solution Here’s a figure that represents the situation.
To find the line’s equation, we’ll need to find the coordinates of the point P, where it intersects the given line on the X-axis. Also, we’ll need its slope. Finally, we can use the point slope form to get the equation. Let’s start with the point.
Since P lies on the X-axis, its y-coordinate must be 0. To find its x-coordinate, we’ll substitute y = 0 in the given line’s equation. We’ll get:
3x + 4(0) = 12
⇒ x = 4
Therefore, the coordinates of P are (4, 0).
Next, we can find the slope of the line, using the condition for two lines to be perpendicular. The slope of the given line equals -3/4. If the required slope is m, then:
m x (-3/4) = -1
⇒ m = 4/3
Finally, the equation of the line is:
(y – 0) = 4/3(x – 4)
⇒ 4x – 3y – 16 = 0
We can also use another method, that I discussed previously (check Method II of Q2 (ii)).
Any line perpendicular to the line 3x + 4y – 12 = 0 will be of the form:
4x – 3y + k = 0
Since the line passes through (4, 0), we have:
4(4) – 3(0) + k = 0
⇒ k = -16
Therefore, the required equation is 4x – 3y – 16 = 0.
I think these examples should be sufficient to get you going with angles between lines. Next, I’ll talk about calculation of the distance of a point from a given line.