In this lesson, I will discuss the case of division of different objects into groups, where groups sizes are identical.
Let’s consider six objects, which are to be divided into two groups of equal sizes.
Using the expression from the previous lesson, you may say that the answer will be \( \frac{6!}{3!3!} \) or 6C3. This is obtained by selecting three objects out from the six, and setting them aside, automatically forming the other group.
But there’s a catch! Recall that while forming groups, we’re not bothered about their order. That is, in the case of 5 objects, formation of groups of sizes 3 and 2 will be the same as 2 and 3.
This is what will lead to extra counting in the case of groups of equal sizes. I’ll show you how.
Suppose, one of the 6C3 selections is Pink, Black and Red, which you set aside, forming a group. And we’ll be left with Blue, Yellow and Green, which form the second group.
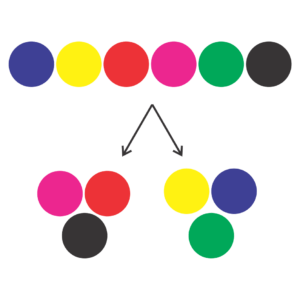
But what if while selecting three objects, we got Yellow, Blue and Green first? Setting these three aside will lead to the same result as above.
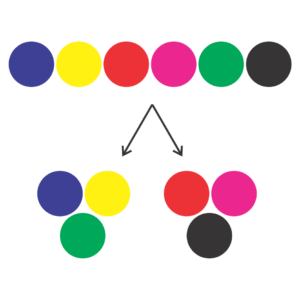
That means, we’ve counted the particular group division [Pink, Black, Red] and [Yellow, Blue, Green] twice. In fact, this will happen with every possible group division. I’ll show another case:
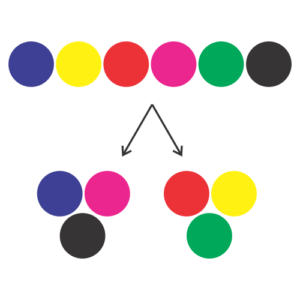 |
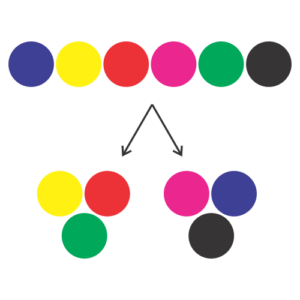 |
The above separation, into groups of [Yellow, Red, Green] and [Pink, Blue, Black] will be counted twice as well.
That means, the number 6C3 calculated earlier will give us double the actual number of group divisions. So, all we have to do is divide 6C3 by 2 to obtain the correct answer, which is 10. I’ll show you all the possible divisions.
 |
 |
Hope that made you happy.
Now what if we had to divide these 6 objects into 3 groups of size 2 each? Have a look.
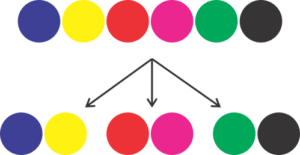
Now the number of group divisions, obtained using the expression from the previous lesson will be \( \frac{6!}{2!2!2!} \)
But due to the fact that the group sizes are identical, the above division, i.e. [Blue, Yellow], [Red, Pink], [Green, Black] will be counted more than once – six times to be precise. I’ll show the six divisions.

That means the actual number of group divisions is \( \frac{1}{6} \times \frac{6!}{2!2!2!} \), as each group division is being counted six times.
Now how do we predict that extra counting, that six? Do you see a pattern there?
If there are three groups of identical size, there are 3! ways of obtaining a particular division.
Because, if we consider one group as an object, then there are three different objects, which can be arranged in 3! ways.
And since we need only one out of these 3!, we divide our answer by 3!.
The same happened in the previous case. There were two groups of the same size, and we divided by 2! or 2.
Now suppose that you have 8 different objects and you need to divide them into three groups of sizes 3, 3, and 2. In how many ways can you do the division?
The number of ways is \( \frac{8!}{3!3!2!} \times \frac{1}{2!} \). Once again, we divided the answer from the previous lesson by 2! as there are 2 groups of equal size.
And if you have 14 different objects and you need to divide them into five groups of sizes 4, 4, 2, 2, and 2?
We’ll take \( \frac{17!}{4!4!2!2!2!} \). and divide it by 2! to take care of the two groups of identical size (4). But we’re not done yet. We still have three more groups of identical size (2). To take care of these, we need to further divide the answer by 3!.
So, our final crazy looking answer is \( \frac{17!}{4!4!2!2!2!} \times \frac{1}{2!3!} \).
I’ll end this lesson there. Think about why we divided the last answer by 2! x 3! and not 5!. The reason remains the same as the very first case. Think about it.
Think.
I’ll give a formula too. But remember that formulas don’t help much in this chapter.
Lesson Summary
- The number of ways to divide n different objects into x groups of size a each, y groups of size b each, and z groups of size c each is equal to \( \frac{n!}{(a!)^x(b!)^y(c!)^zx!y!z!} \), where ax + by + cz = n.
Don’t even think about committing this to memory!
I’ll illustrate the formula’s usage through a few examples in the next lesson.