Division Into Groups: Part 1

Welcome to the next lesson in the Permutation and Combination series. We’ve come a long way, and we have a long way to go. Hope you’re having fun!

This lesson will tackle the following problem

In how many ways can n distinct objects be divided into r groups, whose sizes are known?

Here are a few examples:

In how many ways can we divide 5 different objects into two groups, of sizes 3 and 2?

In how many ways can we divide 10 different objects into three groups, of sizes 3, 2 and 5?

In how many ways can we divide 10 different objects into 5 pairs?

Note that dividing into groups of size 2 and 3 is equivalent to dividing into groups of size 3 and 2. That is, only the sizes matter, not the order of the groups. Similarly dividing 10 objects into three groups of sizes 3, 2 and 5 will be considered same as their division into groups of sizes 2, 3 and 5 or 5, 2 and 3.

Let’s begin with the first case. 5 objects, to be divided into two groups, of size 2 and 3.

Here are the five objects:

And, what we want is this:

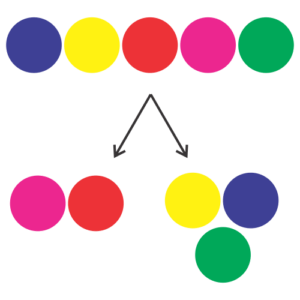
Or, this:

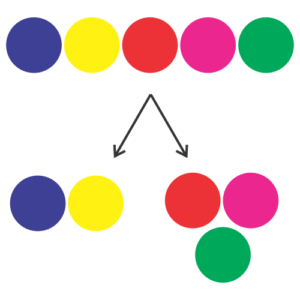How can we find the number of ways to do so?

Well, all you have to do is select 2 objects from the 5 and set them aside, forming a group. And, you don’t have to worry about the second group, as setting aside 2 objects results in 3 objects being left over, which will form the other group.

And, this selection can be done in ⁵C₂ ways or \( \large \frac{5!}{2!.3!} \) ways.

Note that we could also have selected three objects first, leaving behind 2. This could be done in ⁵C₃ ways, which is exactly the same as the previous answer.

Let’s take the second example now. In how many ways can we divide 10 different objects into three groups, of sizes 3, 2 and 5?

The method will be the same as used previously. First, we’ll select 3 objects out of 10, forming the first group. This can be done in ¹⁰C₃ ways.

Next, from the remaining 7 objects, we’ll select 2 objects and form the second group, in ⁷C₂ ways. And, the third group gets formed on its own, as there’ll be 3 objects left over.

The number of ways to perform both these tasks will be ¹⁰C₃.⁷C₂ (using the multiplication principle), which equals \( \large \frac{10!}{3!.2!.5!}\)

And what if a lot of 14 different objects had to be divided into 4 groups of sizes 2,3, 4 and 5?

You guessed it right – the answer will be ¹⁴C₂.¹²C₃.⁹C₄ or \( \large \frac{14!}{2!.3!.4!.5!}\)

We can now arrive at a formula for the same. Let’s say we have n different objects, and we’ve to divide them into r groups of sizes a₁, a₂, a₃, …, a_r. Using the same logic above, the number of ways to do so will be \( \large \frac{n!}{a_1!.a_2!.a_3!…a_r!}\)

A small note. For now, the group sizes will be considered as distinct. That is,

a₁ ≠ a₂ ≠ a₃ ≠ … ≠ a_r

Things will change a bit, if one or more of the groups have the same size. I’ll talk about that in the next lesson.

Lesson Summary

The number of ways to divide n different objects into r groups of sizes a₁, a₂, a₃, …, a_r is equal to

\( \frac{n!}{a_1!a_2!a_3!…a_r!}\)

Here, a₁ ≠ a₂ ≠ a₃ ≠ … ≠ a_r and a₁ + a₂ + a₃ + … + a_r = n.