In this lesson, I’ll cover some simple examples involving the section formula.
Example 1 Find the coordinates of the point which divides the line segment joining A(2, 4) and B(4, 6) in the ratio
(i) 1 : 3 internally
(ii) 1 : 3 externally
Solution The figure illustrates the two cases. Notice that in both cases, AC : CB = 1 : 3.

To find the required point, we just have to substitute in the values in the section formula.
(i) Let’s apply the section formula for internal division:
x = \(\frac{1\times4+3\times2}{1+3}\) = 5/2
y = \(\frac{1\times6+3\times4}{1+3}\) = 9/2
Therefore, the coordinates of the required point are (5/2, 9/2).
(ii) Here, we’ll apply the section formula for external division:
x = \(\frac{1\times4-3\times2}{1-3}\) = 1
y = \(\frac{1\times6-3\times4}{1-3}\) = 3
Therefore, the coordinates of the required point are (1, 3).
The only thing you need to take care of is the order of A and B. The answer would have been different if the question had mentioned B and A instead of A and B. Always draw a figure to avoid any errors.
Example 2 Find the ratio in which the point C(2, 4) divides the line segment joining:
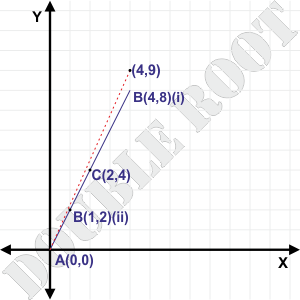
(i) A(0, 0) and B(4, 8)
(ii) A(0, 0) and B(1, 2)
Solution This problem is the opposite of the previous one. The three points are given, and we have to find out the ratio in which one of them divides the line joining the other two.
(i) Let’s assume the ratio to be k : 1. Now, applying the section formula, we can write
2 = \(\frac{k\times4+1\times0}{k+1}\)
This, on solving gives k = 1. Therefore, C divides AB in the ratio 1 : 1 (making it the midpoint of AB).
Wait, but what about the y-coordinate? Let’s check using that too.
4 = \(\frac{k\times8+1\times0}{k+1}\)
Again, we’ll get k = 1.
Hmm. Something’s strange! How did both equations magically gave the same answer? Do they have to?
Let’s change the point B to (4, 9). If we calculate the value of k using the y-coordinate of C now, we’ll get k = 4/5, or the ratio as 4 : 5.
This means that the point C divides the same line segment in two different ratios! That’s not possible.
So what’s wrong then? When B is changed to (4, 9), the three points are not collinear any more. The point C doesn’t even lie on the line joining A and B, forget about dividing it in ratios. That’s why the silly result!
So, in case the two equations (both of which you must solve) give different values of k, it means the points are non-collinear. (That gives us an alternate way to check whether three points are collinear or not. I’ll explain this in a subsequent example.)
(ii) Again, let’s begin by assuming the ratio to be k : 1. Using the section formula, we have:
2 = \(\frac{k\times1+1\times0}{k+1}\)
⇒ k = -2
If we apply the formula to the y-coordinate of C, we’ll get:
4 = \(\frac{k\times2+1\times0}{k+1}\)
⇒ k = -2
What do you think the negative value of k implies? It means that the point C divides AB in the ratio 2 : 1 externally.
Since we’ve assumed in our calculation the division to be internal, the negative value shows that it was actually the opposite. In case we had used the formula for external division, we would have got the value of k as 2.
Here is a figure to illustrate what’s happening.
Example 3 Find the distance between the incentre and the centroid of the triangle whose vertices are (0, 0), (3, 0), and (0, 4).
Solution We’ll first find the centroid, followed by the incentre and calculate the required distance using the distance formula. The centroid is given by
\((\frac{0+3+0}{3},\frac{0+0+4}{3})\) ≡ (1, 4/3)
The sides of the triangle are of lengths 3, 4, and 5 (calculated using distance formula). Therefore, the incentre is given by
\((\frac{5\times0+4\times3+3\times0}{5+4+3}, \frac{5\times0+4\times0+3\times4}{5+4+3})\) ≡ (1, 1)
The required distance equals
\(\sqrt{(1-1)^2+(4/3-1)^2}\) = 1/3
Example 4 Prove that the points A(1, 2), B(3, 10) and C(2, 6) are collinear.
Solution We’ll use the section formula to prove collinearity instead of the distance formula. Remember that three points will be collinear if we’re able to prove that one divides the line joining the other two in some ratio (any ratio).
We’ll assume the ratio in which B divides AC to be k : 1 and calculate the values of k using both x and y coordinates of B. If they’re the same, then we’re done!
The first equation is
3 = \(\frac{k\times2+1\times1}{k+1}\)
⇒ k = -2 (i.e. 2 : 1 externally)
The second equation is
10 = \(\frac{k\times6+1\times2}{k+1}\)
⇒ k = -2
That means B divides AC in the ratio 2 : 1 externally, which is only possible if they are collinear.
Example 5 Show that the points A(0, 0), B(3, 0), C(4, 1), and D(1, 1) form a parallelogram.
Solution This the same problem as 3 (i) in lesson 3. But we’ll solve it using a much better method.
A sufficient condition for ABCD to be a parallelogram is that the diagonal AC and BD bisect each other. This means that AC and BD have the same midpoint.
So, all we have to do is that prove that AC and BD have the same midpoints. We can see that it is actually true. The midpoint of both AC and BD is (2, 1/2), making ABCD a parallelogram.
That’s it for now. A long way to go. Hope you’re enjoying. See you in the next lesson!