Welcome to the third lesson! In this lesson I’ll illustrate some simple problems involving distance formula, followed by some applications. Let us start with the simple ones.
Example 1. Find the distance between
(i) P (3, 1) and Q (-2, -2)
(ii) R (1, 2) and S (-4, 3)
Solution. The following figure gives an idea of the location of the points, and the distances we need to calculate.
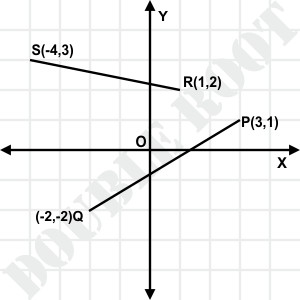
(i) Using the distance formula, we have PQ= \(\sqrt{(-2-3)^2 + (-2-1)^2}=\sqrt{34}\)
(ii) Again, plugging in the values in the formula, we get RS= \(\sqrt{(-4-1)^2 + (3-2)^2} = \sqrt{26}\)
Let us see some more examples.
Example 2. Show that the points
(i) A(0, 0), B(1, √3) and C(2,0) form an equilateral triangle
(ii) P(1, 0), Q(-3, 3) and R(1, 3) form a right angled triangle
Solution. The only tool we have (yet) is the distance formula. So what do you think?
(i) Simple! All we have to show is that AB = BC = CA
AB= \(\sqrt{(1-0)^2 + (\sqrt{3}-0)^2}=2\)
BC= \(\sqrt{(2-1)^2 + (0-\sqrt{3})^2}=2\)
CA= \(\sqrt{(2-0)^2 + (0-0)^2}=2\)
… and we’re done !
(ii) What about this one? Any relation between PQ, QR and PR? Reminds me of Pythagoras ! Let us calculate the sides.
PQ= \(\sqrt{(-3-1)^2 + (3-0)^2}=5\)
QR= \(\sqrt{(1-(-3))^2 + (3-3)^2}=4\)
PR= \(\sqrt{(1-1)^2 + (3-0)^2}=3\)
Clearly, we can see that PR2 + QR2 = PQ2. Therefore the triangle with vertices P, Q and R is right angled (at R).
Here is a figure to illustrate
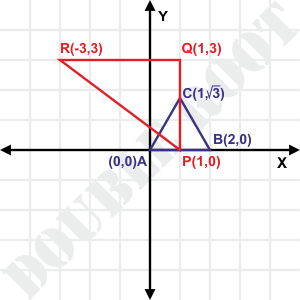
On to some more examples !
Example 3. Show that the points
(i) A(0, 0), B(3, 0), C(4, 1) and D(1, 1) form a parallelogram
(ii) P(0, 0), Q(4, 0), R(4, 1) and S(0, 1) form a rectangle
(iii) K(-1, 0), L(0, -2), M(1, 0) and N(0, 2) form a rhombus
(iv) E (-2, 0), F(0, -2), G(2, 0) and H(0, 2) form a square
Solution. To solve the problem, we need to recall the properties of the above quadrilaterals, in terms of the relation between their sides, and diagonals. I’ll skip the calculations now. Here are figures to illustrate
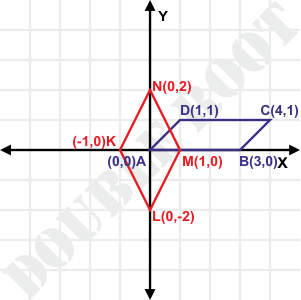
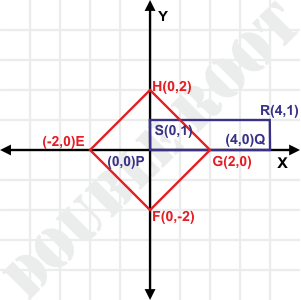
(i) For a paralellogram, both pairs of opposite sides should be equal
AB=3, BC= \(\sqrt{2}\) , CD = 3 and DA= \(\sqrt{2}\)
We can see that, AB = CD and AD = BC .. and we’re done.
(ii) Same conditions as above. Additionally, we need to show that the diagonals are of equal length
Here, PQ = 4, QR = 1, RS = 4 and SP = 1. This makes PQRS a parallelogram.
Now, PR= \(\sqrt{17}\) and also QS= \(\sqrt{17}\) , i.e. the diagonals are equal, which makes PQRS a rectangle.
(iii) Here, all the sides should be equal. We can easily calculate and show that PQ = QR = RS = SQ = \(\sqrt{5}\) , making KLMN a rhombus
(iv) Same conditions as (iii). Plus, the diagonals need to be equal. Here EF = FG = GH = HE = \(\sqrt{8}\) and EG = FH = 4. Therefore EFGH is a square
One more…
Example 4. Show that the points P(1, 3), Q(4, 7) and R(10, 15) are collinear (i.e. lie on a straight line).
Solution. Hmm.. we never talked about collinearity of points.. can we solve this using only distance formula? Turns out we can ! See the following figure
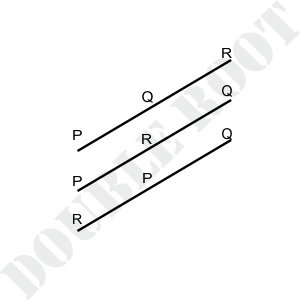
Regardless of the relative positions of P, Q and R one of the following must be true, if they are collinear:
PQ + QR = PR, PR + RQ = PQ or QP + PR = QR.
So what do we need to do? Simply find out PQ, QR and PR, and show that one of them equals the sum of the other two. Here PQ = 5, QR = 10 and PR = 15. We can see that PQ + QR = 15 = PR. We are done !
Last one…
Example 5. Find the area of the triangle whose vertices are P(1, 0), Q(-3, 3) and R(1, 3).
Solution. Well? Recall the Heron’s formula for finding out the area of a triangle
A= \(\sqrt{s(s-a)(s-b)(s-c)}\) , where a,b,c are the lengths of the sides and s=(a+b+c)/2
Here the lengths of the sides PQ, QR and PR are 5, 4 and 3 respectively, which makes s=6. Putting the values in the above formula, we get A \(=\sqrt{6(6-5)(6-4)(6-3)}\) =6
We saw some very simple problems involving the distance formula, and a few applications involving triangles and quadrilaterals. Notice that we proved three points to be collinear (and others geometric results) by using only algebraic expressions and equations. This is what coordinate geometry is all about !
The next lesson will begin with another interesting concept – the section formula.