In this lesson, we’ll establish the formula to find out the distance between two points whose coordinates are given. This formula is commonly known as the Distance Formula.
Distance Formula
Suppose we have two points, P(x1, y1) and Q(x2, y2). What we need to find is the distance between the points P and Q, i.e. the length of PQ.

Before finding that, let’s try to solve simpler versions of the same problem.
When PQ is parallel to the X-axis
Here’s a figure that shows P and Q.

To find PQ, we’ll extend PQ, meeting the Y-axis at R.
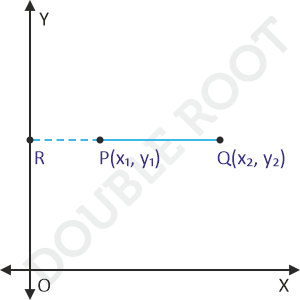
Now, PQ can be expressed as QR – PR.
Since PR is parallel to the X-axis, it will be perpendicular to the Y-axis. Therefore, PR is the perpendicular distance of P from the Y-axis, which is equal to the x-coordinate of P, i.e. x1.
Similarly, QR is the perpendicular distance of Q from the Y-axis, which is equal to the x-coordinate of Q, i.e. x2.
Therefore,
PQ = QR – PR = x2 – x1
What happens if P is to the left of the Y-axis? Or to the right of Q? Will we get the same expression? That’s for you to find out.
In conclusion, when P(x1, y1) and Q(x2, y2) are such that PQ is parallel to the X-axis, then
PQ = |x2 – x1| (i.e. the positive difference between the x-coordinates)
Here’s a simulation which demonstrates the above fact.
Try dragging P and Q, and observe the distance between them. Is PQ always equal to |x2 – x1|?
When PQ is parallel to the Y-axis
Here’s a figure that shows P and Q.

We’ll extend PQ, meeting the X-axis at R.
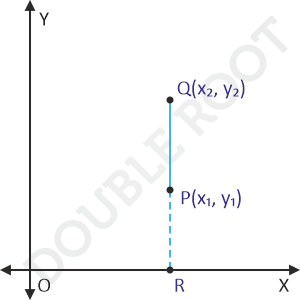
Again, PQ can be expressed as QR – PR.
Since PR is parallel to the Y-axis, it will be perpendicular to the X-axis. Therefore, PR is the perpendicular distance of P from the X-axis, which is equal to the y-coordinate of P, i.e. y1.
Similarly, QR is the perpendicular distance of Q from the Y-axis, which is equal to the y-coordinate of Q, i.e. y2.
Therefore,
PQ = QR – PR = y2 – y1
What happens if P is below the X-axis? Or above Q? Will we get the same expression? Again, you find out!
In conclusion, when P(x1, y1) and Q(x2, y2) are such that PQ is parallel to the Y-axis, then
PQ = |y2 – y1| (i.e. the positive difference between the y-coordinates)
Here’s a simulation which demonstrates the above fact.
Try dragging P and Q, and observe the distance between them. Is PQ always equal to |y2 – y1|?
Now, let’s go back to the original problem.
When PQ is not parallel to any axis

To find PQ, we’ll apply our knowledge from the previous two sections, i.e. somehow express PQ in terms of horizontal and vertical distances. Here’s what we can do.
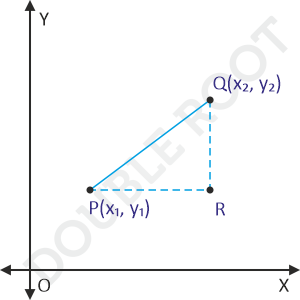
We constructed two line segments, PR and QR, parallel to the X-axis and Y-axis respectively.
Here’s the idea – if we’re able to find the lengths PR and QR, then we can apply Pythagoras’ theorem in ΔPQR to find PQ. That is,
PQ = \(\sqrt{PR^2 + QR^2}\)
To find PR and QR, we need to find the coordinates of R first. Then, we can use the expressions from the previous two sections for the respective lengths.
Now, PR is parallel to the X-axis. This means that the distances of P and R from the X-axis. i.e. their y-coordinates, are the same. Therefore, the y-coordinate of R is y1.
Similarly, QR is parallel to the Y-axis. This means that the distances of Q and R from the Y-axis. i.e. their x-coordinates, are the same. Therefore, the x-coordinate of R is x2.
And so, we’ve found the coordinates of R as (x2, y1).
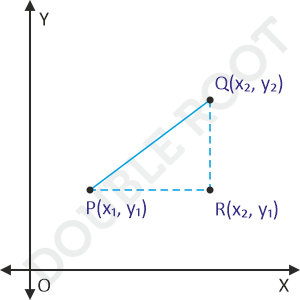
Now, PR and QR are easy to find:
PR = x2 – x1
QR = y2 – y1
And, we’re done! Having obtained PR and QR, we can finally find the distance PQ:
\(PQ = \sqrt{PR^2 + QR^2} \)
\(\Rightarrow PQ =\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}\)
Awesome! We just derived the Distance Formula.
Here’s a simulation that shows two points and the distance between them.
Try dragging the points and observe the length PQ. Do you get the same value when you apply the distance formula for the two points?
Lesson Summary
The distance between two points P(x1, y1) and Q(x2, y2) is given by
\(PQ = \sqrt{( x_2 – x_1)^2 + (y_2 – y_1)^2}\)
This formula is known as the Distance Formula. The next lesson will cover some examples and applications.