7. Area of a Polygon

In this lesson, we’ll discuss how to find the area of a triangle, whose vertices are given. Then, we’ll extend it to finding the area of any polygon.

Let’s start with the triangle. You’ve already seen one (tedious) method of finding the area, which involved the distance formula. Here is a better one.

Area of a Triangle

Suppose the triangle’s vertices are A(x1, y1), B(x2, y2), and C(x3, y3). Let’s start with some constructions.

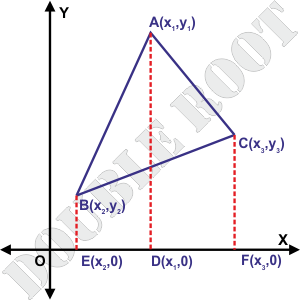
Coordinate Geometry - Area of a Triangle

The idea here is to express the area of the triangle ABC, in terms of other areas which can be calculated much easily. These are the areas of the trapeziums ABED, ADFC and BEFC. The required area , Ar(ABC) = Ar(ABED) + Ar(ADFC) – Ar(BEFC)

Now, Ar(ABED) = ED.(BE + AD)/2 which equals (x2 – x1)(y2 + y3)/2

Similarly, the other areas can be found out, and after putting in the values we get:
Ar(ABC) = 1/2[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
This can also be written as:
1/2[(x1y2 – x2y1) + (x2y3 – x3y2) + (x3y1 – x1y3)]
The former expression is easier to remember. Note that this expression assumes that A,B and C are in anticlockwise order. Had they been clockwise order, this expression would have given the same answer with a negative sign. So we have two options to get the right answer, either ensure that the points are taken in anticlockwise order, or take the absolute value of the expression.

Moving on to polygons.

Area of a Polygon

The method of finding the area remains the same. I’ll first illustrate finding out the area of a quadrilateral, and generalize the method it to a n-sided polygon.

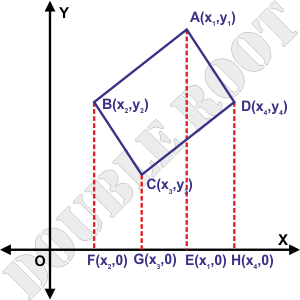
Coordinate Geometry - Area of a Quadrilateral

The required area can again be expressed in the terms of the trapeziums’ areas.

Ar(ABCD) = Ar(ABFE) + Ar(AEHD) – Ar(BFGC) – Ar(CGHD)

Putting in the values, we get:

Ar(ABCD) = 1/2[(x1y2 – x2y1) + (x2y3 – x3y2) + (x3y4 – x4y3) + (x4y1 – x1y4)] (similar to the second expression I mentioned for the triangle)

Similarly, suppose we have a polygon of n sides whose vertices, taken in anticlockwise order, are:

(x1, y1), (x2, y2), (x3, y3), … (xn, yn)

Then, the area of the polygon equals:

1/2[(x1y2 – x2y1) + (x2y3 – x3y2) + … + (xny1 – x1yn)]

Lesson Summary

  1. The area of a triangle whose vertices (taken in anticlockwise order) are (x1, y1), (x2, y2) and (x3, y3) is given by (1/2)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
  2. The area of an n-sided polygon whose vertices (taken in anticlockwise order) are (x1, y1), (x2, y2) … (xn, yn) is given by (1/2)[(x1y2 – x2y1) + (x2y3 – x3y2) + …… + (xny1 – x1yn)]

That’s it for now! See you in the next lesson with some examples.

Leave a Reply

Scroll to Top