Definition and Standard Equation

Welcome to the first lesson in the Circle series.

This lesson will begin with the definition of a circle. Then, using this definition, we’ll derive the standard equation of a circle.

Let’s begin!

Definition of a Circle

A circle is a set of all points in a plane, which are equidistant from a fixed point.

• The fixed point is known as the center of the circle.
• The distance between the center and any point on the circle is known as the radius of the circle.

In slightly technical words, a circle is the locus of a point, moving in a plane, such that its distance from a fixed point is always constant. This fixed point is the center of the circle, and this constant distance is the circle’s radius.

Standard Equation of a Circle

We’ll derive the standard equation to a circle – which has the center as origin (0, 0) and radius equal to r.

Let P(x, y) be any point on the circle. Then, according to the definition of the circle, the distance between P and O will always be equal to r. That is, OP = r.

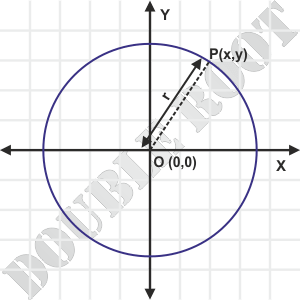
Using the distance formula, we can rewrite the above relation as:

√((x – 0)² + (y – 0)²) = r

On squaring both sides, we get the equation of the circle as:

x² + y² = r²

And that’s the standard equation of the circle.

Lesson Summary

1. The equation of the circle, having center as origin and radius r, is given by x² + y² = r².

In the next lesson, I’ll cover a few more forms of the equation of a circle.